1)信號的分解
通常小波分解與重構可以通過Mall算法來實現,{Vt}是L²(R)中的一個多尺度分析,Φ爲尺度函數,{Ψƒ,n}ƒ,n爲小波基,則通過Mallat算法有分解式:
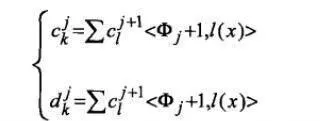
可以簡記爲:
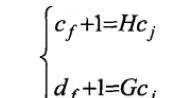
上式中,H和G分別爲低通濾波器和高通濾波器。將CO定義爲原始信號X,於是k以將X分解爲d1, d2,…dj和cj(j爲最大分解層數),cj和dj分別稱爲原始信號在分辨率洲2 -j的逼近信號和細節信號。各層細節信號和逼近信號是原始信號X在相鄰的不同頻率段上的成分。
採用Mallat算法進行小波分解,每一次分解後得到的細節信號和通近信號比分解前的信號點數減少一倍,經平滑處理後,用Mallat算法將分解後的信號進行重構。
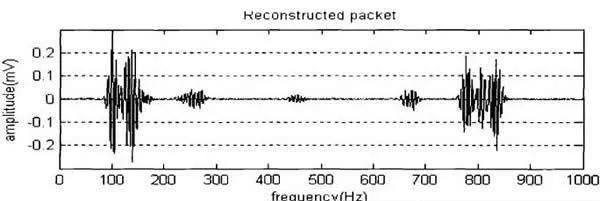
2)信號的重構
重構算法描述如下:
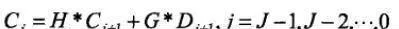
其中,H*和G*分別是H和G的對偶算子,採用重構算法對小波分解後的信號進行重構可以增加信號的點數。對d1,d2,…dj和cj分別進行重構後,得到D1, D2,
…Dj和Ci,且D1={d11,d12,…djn},…DJ={dj1, dj2,…djn},Cj={Cj1,Cj2,… Cjn},它們和原始信號X的點數一樣,並且有:
X=D1+D2+…+DJ+|CJ
式中D1,D2,…Dj,分別爲第一層、第二層、…、第J層細節信號的重構結果,Xj:{XJ1,XJ2,…,XJN}爲第J層逼近信號的重構結果,因此:
Xji=D1,i+D2,i+…+Dj,i+|CJ,i