交易員所面臨的最嚴重的問題之一就是有可能發生災難性的虧損。災難性的虧損是指超過交易員預算的虧損,它遠大於交易所需的投資資金或者保證金。曾經發生過一筆糟糕的交易在金融領域而毀滅一個交易員這樣的事情。毫無疑問,悲劇還會上演。
針對災難性風險,有兩種普遍的看法。第一種看法認爲交易員實際上承受痛苦的概率很小,甚至幾乎不值得考慮這些風險;第二種看法認爲,一個人會損失其大半財富的這種可能性足以警戒所有人,除了那些有勇無謀的魯莽者。
兩種看法都有可取之處。很顯然,每個交易員和潛在的交易員都應該仔細思考承擔災難性虧損的可能性。同時,那些發現自己很難接受這樣的可能性的人應該避免冒險。
災難性風險是指交易員除了損失交易資金之外所要承擔的風險。顯而易見,如果交易員將所有資產投入交易,他沒有承擔任何災難性風險,許多年輕的交易員都是這麼做的。如果交易員有130000美元資產,而將其中的100000美元投入交易,他就不必過多地擔心災難性虧損。如果交易員蒙受了500000美元的虧損,他就破產了,但是破產和一系列虧損交易沒有多大區別。這種方法對大多數交易員來講都不是審慎的方法,尤其是那些年老的交易員,或者企業交易者。
對大多數交易員而言,一個更有用的途徑是保護一部分資產以防被扣押。我知道投資者有多種方式來保護資產。例如,將資金放入合格的養老計劃中就很安全,直到退休。將資金放入短期信託中就很安全,直到資金迴流到創造者手裏。在虧損前將資金轉給其他的家庭成員很安全,但是資金就不再是給予者的了。
或者,由一個全資公司進行交易,而不是由交易員來進行交易。通過限制股東或者公司官員的欺詐,公司的股東僅對投入資本和他們作出的保證負責。當然,交易員可能已經是某個養老計劃或者保本基金的法人,他不想冒險投入所有資金,這樣一來,公司就能分拆一個全資子公司。由於法律比市場還要多變,交易員應該在通過法律途徑保護資金前諮詢律師。
如果交易員不能保護大部分的資產,他就應該花上半個小時左右的時間想象一旦虧損是自己能冒險資金量的十倍,會發生什麼。他感覺如何?他的妻子感覺如何?他的孩子和鄰居感覺如何?如果他是一個公司的職員,他的老闆或者董事會將感覺如何?這些人會怎麼做?他對這些人的感覺會作何感想?他不得不採取哪些行動?
毫無疑問,災難性虧損相當可怕。對許多人而言,沒有潛在的利潤值得冒險。對另一些人而言,如果承擔災難性虧損的概率足夠小交易值得冒險。這是一個重要的前提條件。許多交易員斷然不會接受這樣的風險。的確,許多交易員閱讀本章是因爲他們不想要這些風險。但是這並不能完全消除風險。必須有人承擔這些風險。許多時候,這不是慈善行爲甚至是愚蠢的行爲。更多時候,承擔風險的個人或者公司會因此得到回報。考慮到大多數投資者是多麼強烈地想要避免風險,承擔風險的投資者很可能回報頗豐。
只有報酬相對大於風險時,才值得賣給其他交易員類似災難性虧損保險的產品。但是風險有多大呢?
經濟學家曾經認爲他們確切瞭解任何價格變化的可能性。那時,經濟學家相信股票和商品價格變化呈正態分佈。如果價格變化事實上是正態分佈,知道分佈的平均數和標準差,那麼我們就能知道該分佈的所有信息。
的確,如果價格變化實際上呈正態分佈,超過距平均數三個標準差的價格變化出現的概率應小於0.01;而超過十個標準差的價格變化應該幾乎不會發生。如果價格變化呈正態分佈,災難性風險就不會是個嚴重的問題。
不幸的是,災難性風險是一個嚴重的問題。
當曼德布羅特宜布某些投機價格不是正態分佈時,經濟學家們都很震驚。這些分佈看上去是正態分佈,而且,有強有力的數學原因能證明爲什麼這些分佈應該是正態分佈。儘管如此,曼德布羅特還是堅持它們不是正態分佈。曼德布羅特注意到,分佈的尾部比在正態分佈情況下要更密集,因此,事實上分佈不呈正態分佈。
曼德布羅特相信正確的分佈是一個穩定帕累託分佈。這一論斷沒有得到很多贊同。我們已經徹底研究了正態分佈的數學運算,但卻不瞭解穩定帕累託分佈的數學運算。
的確,我們只真正瞭解三種特殊情況的分佈:擲硬幣、正態分佈和柯西分佈(我們稍後討論)。這些例子實際上都相對簡單。的確,所有這三種分佈都能通過兩個變量來完全描述,例如平均數和標準差。
另一方面,穩定帕累託分佈需要四個變量才能描述一個分佈:位置、尺度、斜度和峯度。位置是分佈的居中趨勢,可以由平均數或者中位數測量。尺度是分佈的寬度或者分散度,可以由標準差或者絕對偏差均值測量。斜度是分佈的對稱性(如圖9-1),峯度是分佈尾部的密集度(如圖9-2)。
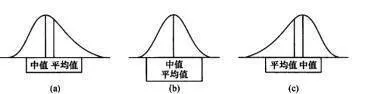
圖9-1斜度可以是正向的(a)、不存在(b)或者負向的(c)
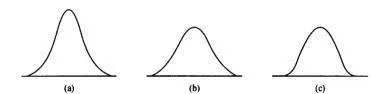
圖9-2峯度可以呈尖峯狀(a)、不存在(b)或者平頂狀(c)
該分佈最重要的變量就是峯度。分佈的峯度決定了使用哪種統計工具來測量其他的三個變量。一個穩定帕累託分佈的峯度(X)由一個介於0至2的量表來測量,不包括0,包括2。當分佈呈對稱,且X等於2時,該分佈就呈正態分佈。當分佈是正態分佈時,平均數就是位置的有效測量,標準差就是分散度的有效測量。
然而,當X小於2,標準差很快就變得沒有意義了。所幸只要X大於1,絕對偏差均值就是分散度的有效測量;而不幸的是,只要X大於1,絕對偏差均值和平均數就是唯一有效的測量量。當X等於1且分佈是對稱時,該分佈就是柯西分佈。當分佈是柯西分佈時,或者更一般地講X小於等於1時,理性交易就變得相當困難了(如圖9-3)。
問題是沒有真正理想的、有用的有效測量能夠確定類似柯西分佈的分佈位置。最理想的測量量就是算術平均數,即平均數。但是當X小於等於1時,平均數不是一個有效的測量量。這意味着一個過去可獲利的交易方法無法保證持續帶來利潤。樣本容量爲十億與樣本容量爲1一樣有用,也一樣沒用。

圖9-3正確的商品價格分佈
解圖:正確的商品價格分佈似乎處於正態分佈和柯西分佈之間,如果我們能忽略斜度。但學生t分佈,穩定帕累託分佈的分佈,以及其他分佈和家族分佈都包括這一範圍。
我們仍然能夠測量位置。例如,中位數仍然可以有效測量類似柯西分佈的分佈。它沒有真正告訴交易員想知道的事情,當我們無法獲知平均數時,僅能知道中位數,然而,中位數並非理想的測量量。
所幸價格看上去不是一個柯西分佈,至少我所知道的已發表的價格行爲研究文獻中沒有這樣的例子。不幸的是,X的估值在樣本與樣本之間差異極大,所以我們很難準確地說X是什麼,儘管它似乎介於1和2之間(見表9-1)。
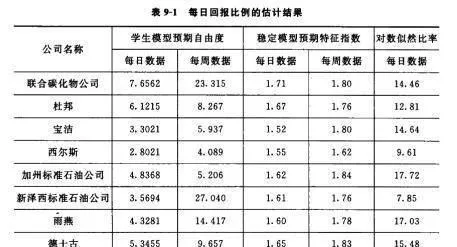
表9-1每日回報比例的估計結果
有趣的是,穩定帕累託分佈並非只能描述從正態分佈到柯西分佈的分佈,學生分佈也能描述,而且我們更瞭解學生分佈。
換句話說,在某種程度上災難性虧損是可以規避的。
我們既有戰略又有策略來消除災難性風險,或者將其最小化。戰略方法不包括預測,策略方法包括預測。我們先來討論戰略方法。