IFS系统
迭代函数系统(IFS)方法是美国佐治亚理工学院的巴恩斯利等人首先应用一组收缩仿射变换生成分形图像，即通过对原始图形(生成元)的收缩、旋转、平移等变换形成的极限图形而具有自相似的分形结构，并将该仿射变换集称为IFS。它与复平面上了ƒ（z)=z²+c为复数)迭代产生的分形存在着内在的联系，只是ƒ(z)属于非线形变换，而IFS属于线形变换。
IFS系统的理论与方法是分形自然景观模拟及分形图像压缩的理论基础，其基本思想是认为物体的全局和局部在仿射变换的意义下具有自相似结构，这就形成了著名的拼接定理。IFS方法的魅力在于它是分形迭代生成的反问题，根据拼接定理，对于一个给定的图形(比如一幅图片)，求得几个生成规则，就可以大幅度压缩信息。
IFS系统生成图形的基本原理
二维空间R²上的线形变换ω具有如下形式：
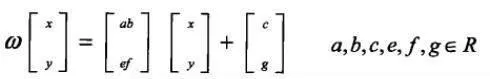
对于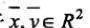
若存在压缩因子s满足0<s<1，使得下式：
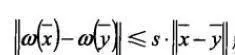成立，则称ω为收缩仿射变换。该变换又可表示为：
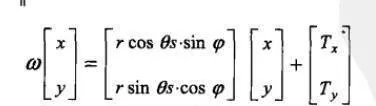
迭代函数系统由一组收缩仿射变换倾{ω1，ω2，ω3，…ωn}组成，二维IFS可以表示为：
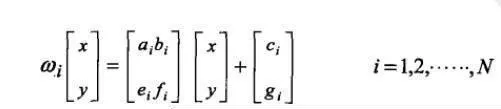（1）
生成图形时，调用各变换的概率：
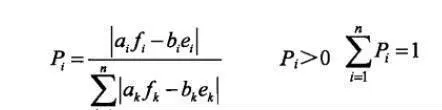（2）
通过公式(1)可以生成许多构成分形图形的点，公式(2)主要是由规则的概率控制生成图形的形态。
IFS系统主要算法
对于IFS系统生成分形图像来说，随机迭代算法是一种高效的算法。鉴于此，在程序的实现过程中，采用了随机迭代算法。随机迭代算法是产生许多的点来构成整个的图像，这些点是循环不断地、随机地生成的。因此，在程序的编制中，可以采用线程的方法来控制点的产生速度，以及控制点什么时候产生和什么时候结束。当然，运用线程会大量消耗CPU的时间。值得一提的是，CPU的速度决定点生成的快慢。
迭代函数系统是分形图案的生成方法之一，它在分形重构方面取得的进展引起了图像压缩技术的革新，达到了用常规压缩方法无法达到的高压缩比。其主要的思想在于存储生成图像的IFS系统，而不存储生成的图像，恢复时根据IFS系统用专门的硬件生成图像。作为产生分形的方法之一，迭代函数系统在自然景物模拟及图像压缩方面具有独到之处，是一个可行的、有价值的研究领域。