IFS系統
迭代函數系統(IFS)方法是美國佐治亞理工學院的巴恩斯利等人首先應用一組收縮仿射變換生成分形圖像，即通過對原始圖形(生成元)的收縮、旋轉、平移等變換形成的極限圖形而具有自相似的分形結構，並將該仿射變換集稱爲IFS。它與複平面上了ƒ（z)=z²+c爲複數)迭代產生的分形存在着內在的聯繫，只是ƒ(z)屬於非線形變換，而IFS屬於線形變換。
IFS系統的理論與方法是分形自然景觀模擬及分形圖像壓縮的理論基礎，其基本思想是認爲物體的全局和局部在仿射變換的意義下具有自相似結構，這就形成了著名的拼接定理。IFS方法的魅力在於它是分形迭代生成的反問題，根據拼接定理，對於一個給定的圖形(比如一幅圖片)，求得幾個生成規則，就可以大幅度壓縮信息。
IFS系統生成圖形的基本原理
二維空間R²上的線形變換ω具有如下形式：
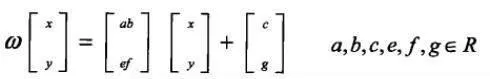
對於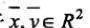
若存在壓縮因子s滿足0<s<1，使得下式：
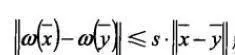成立，則稱ω爲收縮仿射變換。該變換又可表示爲：
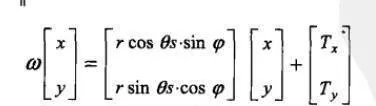
迭代函數系統由一組收縮仿射變換傾{ω1，ω2，ω3，…ωn}組成，二維IFS可以表示爲：
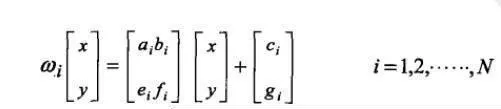（1）
生成圖形時，調用各變換的概率：
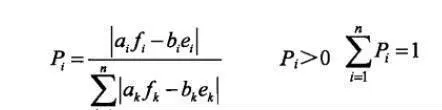（2）
通過公式(1)可以生成許多構成分形圖形的點，公式(2)主要是由規則的概率控制生成圖形的形態。
IFS系統主要算法
對於IFS系統生成分形圖像來說，隨機迭代算法是一種高效的算法。鑑於此，在程序的實現過程中，採用了隨機迭代算法。隨機迭代算法是產生許多的點來構成整個的圖像，這些點是循環不斷地、隨機地生成的。因此，在程序的編制中，可以採用線程的方法來控制點的產生速度，以及控制點什麼時候產生和什麼時候結束。當然，運用線程會大量消耗CPU的時間。值得一提的是，CPU的速度決定點生成的快慢。
迭代函數系統是分形圖案的生成方法之一，它在分形重構方面取得的進展引起了圖像壓縮技術的革新，達到了用常規壓縮方法無法達到的高壓縮比。其主要的思想在於存儲生成圖像的IFS系統，而不存儲生成的圖像，恢復時根據IFS系統用專門的硬件生成圖像。作爲產生分形的方法之一，迭代函數系統在自然景物模擬及圖像壓縮方面具有獨到之處，是一個可行的、有價值的研究領域。