背馳的再分辨
背馳問題說過多次,但發現還有很多誤解。不妨用最典型的a+A+b+B+c爲例子把一些經常被混淆的細節進行說明。
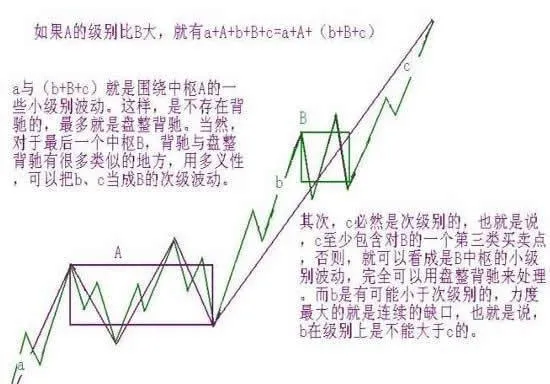
沒有趨勢,沒有背馳,不是任何a+A+b+B+c形式的都有背馳的。當說a+A+b+B+c中有背馳時,首先要a+A+b+B+c是一個趨勢。而一個趨勢,就意味着A、B是同級別的中樞,否則,就只能看成是其中較大中樞的一個震盪。例如,如果A的級別比B大,就有a+A+b+B+c=a+A+(b+B+c),a與(b+B+c)就是圍繞中樞A的一些小級別波動。這樣,是不存在背馳的,最多就是盤整背馳。當然,對於最後一箇中樞B,背馳與盤整背馳有很多類似的地方,用多義性,可以把b、c當成B的次級波動。但多義性只是多角度,不能有了把b、c當成B的次級波動這一個角度,就忘了a+A+b+B+c是趨勢且A、B級別相同的角度。多義性不是含糊性,不是怎麼幹怎麼分都可以,這是必須不斷反覆強調的。
其次,c必然是次級別的,也就是說,c至少包含對B的一個第三類買賣點,否則,就可以看成是B中樞的小級別波動,完全可以用盤整背馳來處理。而b是有可能小於次級別的,力度最大的就是連續的缺口,也就是說,b在級別上是不能大於c的。例如,如果b是次級別,而c出現連續缺口,即使c沒完成,最終也延續成次級別,但c是背馳的可能性就很小了,就算是,最終也要特別留意,出現最弱走勢的可能性極大。
還有,如果a+A+b+B+c是上漲,c一定要創出新高;a+A+b+B+c是下跌,c一定要創出新低。否則,就算c包含B的第三類買賣點,也可以對圍繞B的次級別震盪用盤整背馳的方式進行判斷。對c的內部進行分析,由於c包含B的第三類買賣點,則c至少包含兩個次級別中樞,否則滿足不了次級別離開後次級別回拉不重回中樞的條件。這兩個中樞構成次級別趨勢的關係,是最標準最常見的情況,這種情況下,就可以繼續套用a+A+b+B+c的形式進行次級別分析確定c中內部結構裏次級別趨勢的背馳問題,形成類似區間套的狀態,這樣對其後的背馳就可以更精確地進行定位了。