線段概要
線段是纏論中在筆基礎之上的又一個重要概念。掌握線段的定義和劃分原則,是下一步理解和掌握走勢中樞的必要基礎。
線段定義:連續的三筆之間若存在重疊部分,其起點和終點之間的連線爲線段。
如圖1-65所示,圖左AB、BC、CD爲連續的三筆,它們之間存在重疊部分(陰影部分),AD的連線就叫線段。
圖右EF、FG、GH爲連續的三筆,它們之間存在重疊部分(陰影部分),EH的連線就叫線段。
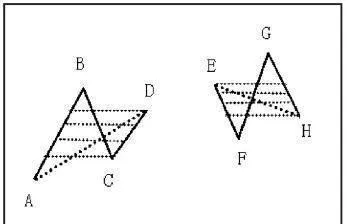
圖1-65
注意:當連續的三筆之間沒有重疊部分時,不能將其連線視爲線段。
如圖1-66所示,圖左AB、BC、CD爲連續的三筆,它們之間不存在重疊部分,AD的連線就不是線段。圖右EF、FG、GH爲連續的三筆,它們之間不存在重疊部分,EH的連線就不是線段。
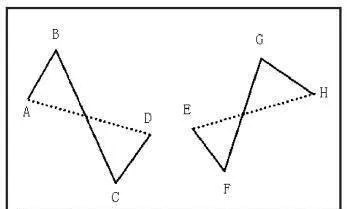
圖1-66
線段必須由連續的三筆構成,這是因爲線段和筆一樣,必須由頂和底來構成,同一性質的兩頂或兩底,不但不能構成筆,也不能構成線段。這是連續的兩筆不能構成線段的原因。
如圖1-67所示,AB與BC是連續的兩筆,但AC的連線不能構成線段,因爲A和C同爲兩個底分型的底。
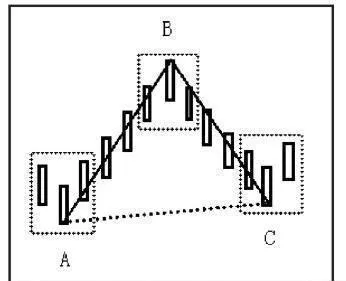
圖1-67
如圖1-68所示,XY與YZ是連續的兩筆,但XZ的連線不能構成線段,因爲X和Z同爲兩個頂分型的頂。
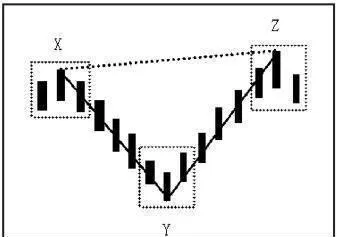
圖1-68
由此可見,線段中包含筆的數目都是單數,雙數的筆都不能構成線段。
圖1-69中,AB、BC、CD是連續的三筆,且有重疊部分,AD連線就是線段。該線段以向上筆開始,稱爲向上線段。
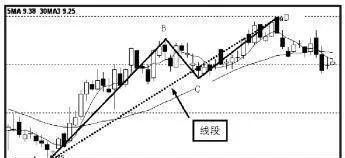
圖1-69
圖1-70中,AB、BC、CD是連續的三筆,且有重疊部分,AD連線就是線段。該線段以向下筆開始,稱爲向下線段。
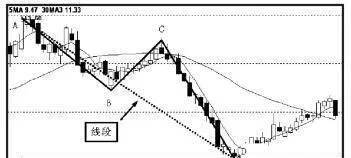
圖1-70