什么是概率分布?
概率分布是一种统计函数,描述随机变量在给定范围内可能取的所有可能值和可能性。该范围将限制在最小和最大可能值之间,但可能值可能绘制在概率分布上的精确位置取决于许多因素。这些因素包括分布的平均值、标准差、偏度和峰度。
概率分布如何运作
也许最常见的概率分布是正态分布或“钟形曲线”,尽管存在几种常用的分布。通常,某些现象的数据生成过程将决定其概率分布。这个过程称为概率密度函数。
概率分布还可用于创建累积分布函数 (CDF),该函数累积出现的概率,并且始终从 0 开始到 100% 结束。
学者、金融分析师和基金经理等可以确定特定股票的概率分布,以评估该股票未来可能产生的预期回报。股票的回报历史可以从任何时间间隔进行衡量,但很可能只包含股票回报的一小部分,这将使分析受到抽样误差的影响。通过增加样本量,可以显着减少该误差。
要点
- 概率分布描述了给定数据生成过程的可能值的预期结果。
- 概率分布有多种形状,具有不同的特征,如均值、标准差、偏度和峰度所定义。
- 投资者使用概率分布来预测股票等资产随着时间的推移的回报并对冲风险。
概率分布的类型
概率分布有许多不同的分类。其中一些包括正态分布、卡方分布、二项分布和泊松分布。不同的概率分布服务于不同的目的并代表不同的数据生成过程。例如,二项式分布评估在给定次数的试验中事件多次发生的概率,并给出每次试验中事件的概率。可以通过记录篮球运动员在一场比赛中罚球的次数来生成,其中 1 = 投篮,0 = 投失。另一个典型的例子是使用一枚均匀的硬币,并计算出该硬币连续抛 10 次后正面朝上的概率。二项式分布是离散的,而不是连续的,因为只有 1 或 0 是有效响应。
最常用的分布是正态分布,常用于金融、投资、科学和工程。正态分布完全由其均值和标准差来表征,这意味着分布没有偏斜并且确实表现出峰度。这使得分布对称,并且在绘制时被描绘为钟形曲线。正态分布的定义是均值(平均值)为零,标准差为 1.0,偏斜为零,峰度 = 3。在正态分布中,大约 68% 收集的数据将落在 +/- 1 个标准范围内平均值的偏差;大约 95% 在 +/- 两个标准偏差内; 99.7% 在三个标准差之内。与二项分布不同,正态分布是连续的,这意味着所有可能的值都被表示(而不是只有 0 和 1,中间没有任何值)。
投资中使用的概率分布
股票收益通常被认为是正态分布的,但实际上,它们表现出峰度,具有较大的负收益和正收益,似乎比正态分布预测的要多。事实上,由于股票价格的界限为零,但具有潜在的无限上涨空间,股票回报的分布被描述为对数正态分布。这显示在股票收益图上,分布的尾部具有更大的厚度。
概率分布也经常用于风险管理,并根据历史收益的分布来评估投资组合发生损失的概率和金额。投资中使用的一种流行的风险管理指标是风险价值(VaR)。 VaR 产生给定投资组合的概率和时间范围内可能发生的最小损失。或者,投资者可以使用 VaR 获得一定损失金额和时间范围内的损失概率。滥用和过度依赖VaR被认为是 2008 年金融危机的主要原因之一。
概率分布的示例
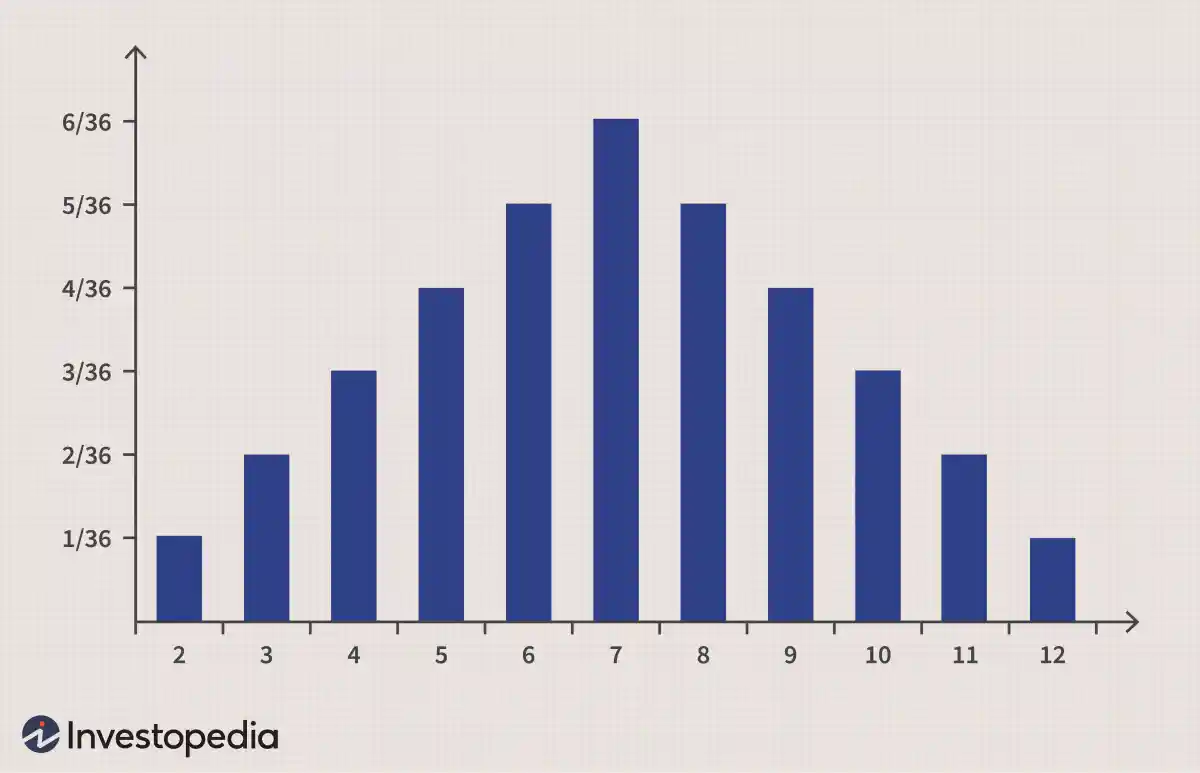
作为概率分布的一个简单示例,让我们看一下掷两个标准六面骰子时观察到的数字。每个骰子都有 1/6 的概率滚动任何单个数字(1 到 6),但两个骰子的总和将形成下图所示的概率分布。七是最常见的结果(1+6、6+1、5+2、2+5、3+4、4+3)。另一方面,二和十二的可能性要小得多(1+1 和 6+6)。