儘管具體討論正態分佈的概念已經超出了道氏理論的範圍,但是爲了將趨勢的含義闡述清楚,作必要的延伸也未嘗不可。因此,這裏不可避免地涉及一些數學概念。
一個理論如果能夠用數學來表現,將代表這個理論的成熟。由於道氏理論本身就具有許多的數學思想,所以它可以用正態分佈論述基本運動的數學特徵,並以正態分佈作爲基本運動宏觀技術分析的核心。
之所以要引用數學概念,是由於在數學中,正態分佈是有嚴格定義的,設連續隨機變量x的概率密度爲:
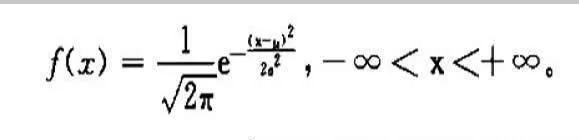
圖1正態分佈論述基本運動的數學特徵
其中5μ,σ(σ>0)爲常數,則稱X服從爲μ,σ的正態分佈或高斯(Gauss)分佈,記爲X~ n(μ,σ²)。
如圖2所示,由於正態分佈圖形有明顯的近似直線部分和頂部與底部部分,所以利用正態分佈圖形我們可以很容易地對應到基本運動的幾個階段—上升趨勢和下降趨勢的底部和頂部。
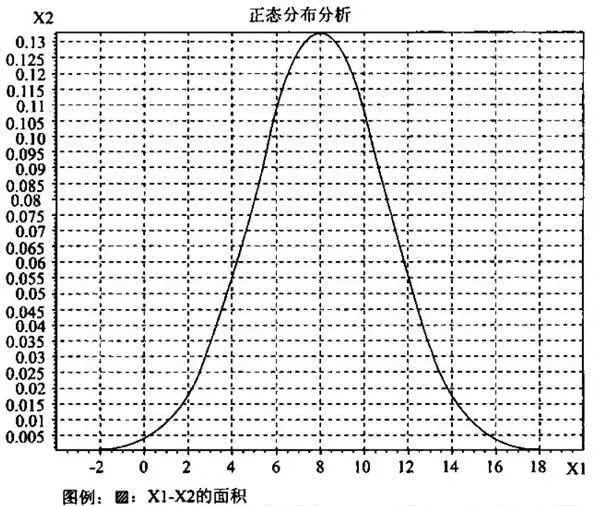
圖2正態分佈曲線圖
另外,對稱也是正態分佈的特徵,即上升趨勢與下降趨勢是對稱的。如果將以上所描述的基本運動的特徵用圖形來表示,則基本運動具有近似正態分佈的特徵。因此我們不難理解:爲什麼道氏認爲牛市、熊市的持續時間是相等的,以及在許多技術圖形中總是出現那麼多的對稱圖形。
同時,用正態分佈的圖形也可以說明:爲什麼股價在頂部的時間短,而在底部的時間長。