什麼是概率密度函數 (PDF)?
概率密度函數 (PDF) 是一種統計表達式,定義某些結果發生的概率。在此函數中,概率是數據集分佈落在兩個標準之間的百分比。
金融分析師使用 PDF 來了解回報如何分配,以評估投資價格和回報的風險和預期。
要點
- 概率密度函數是一種統計度量,用於衡量投資獲得落在一定值範圍內的回報的可能性並表明所涉及的風險。
- PDF 通常繪製在類似於鐘形曲線的圖表上,數據位於曲線下方。
- 兩端的傾斜曲線表示風險/回報較大或較小。
瞭解概率密度函數 (PDF)
概率密度函數衡量投資回報落在指定範圍內的頻率。 PDF 通常用圖表來描述,正常的鐘形曲線表示中性市場風險,兩端的傾斜曲線表示較高或較低的風險回報。
偏度是曲線較高部分向右或向左的偏移。如果曲線向左移動且右側有長尾(右偏),分析師認爲這表明存在更大的上行回報。如果它向右移動,長尾向左(左偏),分析師認爲存在更大的下行風險。
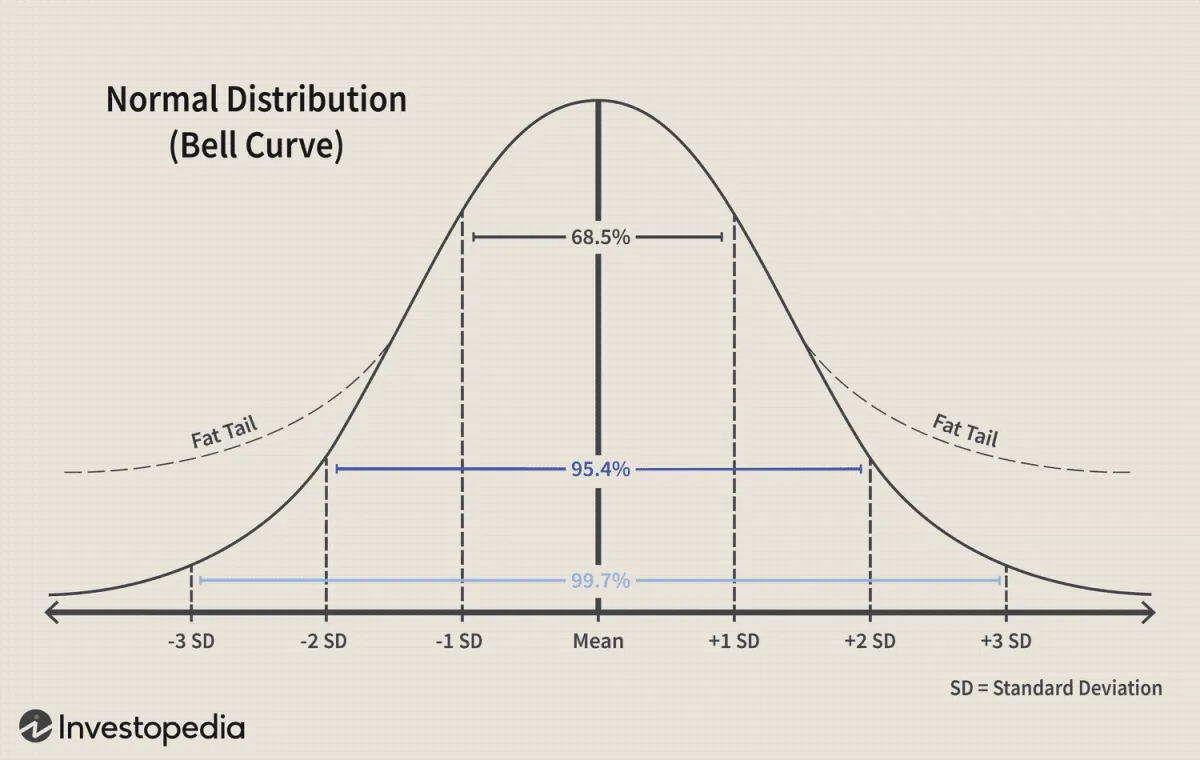
下圖展示了具有鐘形曲線的正態分佈數據。數據平均值是中間的線,垂直線是標準差,或者數據偏離平均值的距離。
平均值兩側的前兩條垂直線顯示 68.5% 的數據落在平均值 +/-1 標準差範圍內。因此,如果這是一條正態分佈的股票收益曲線,您會發現 68.5% 的情況下,收益落在 -1 SD 和 +1 SD 線之間,並且市場風險是中性的(沒有偏斜)。
您應該注意,投資回報很少(如果有的話)呈正態分佈,因此圖表可能永遠不會是乾淨的正態分佈曲線。
計算PDF
計算 PDF 並以圖形方式繪製它可能涉及使用微分方程或積分的複雜計算。在實踐中,需要圖形計算器或統計軟件包來計算概率密度函數。
概率密度函數的示例
概率密度函數衡量的是連續變量——股票和投資回報一般不是連續隨機變量;它們是離散的。然而,大多數金融分析師假設回報和價格是連續的,以便他們可以對績效進行建模並分析風險。
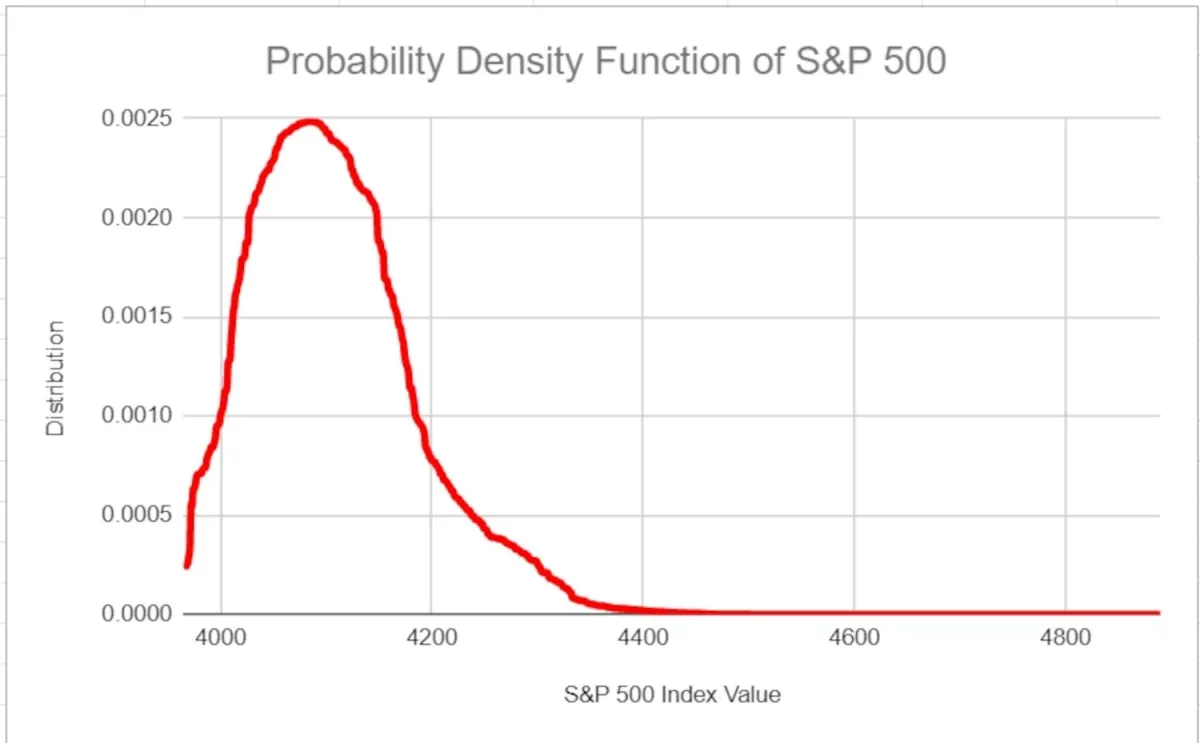
下圖中,對 2020 年 5 月 20 日至 2023 年 5 月 19 日的標準普爾 500 指數值進行了排序和繪製。結果是一條右偏的鐘形曲線,表明過去三年有可能獲得更大的上行回報。
概率密度函數 (PDF) 告訴我們什麼?
概率密度函數 (PDF) 描述了觀察到數據生成過程產生的某些結果的可能性。 PDF 可以告訴我們哪些值最有可能出現,哪些值出現的可能性較小。這將根據 PDF 的形狀和特徵而變化。
什麼是中心極限定理 (CLT) 以及它與 PDF 有何關係?
中心極限定理 (CLT)指出,隨着樣本量變大,樣本中隨機變量的分佈將開始接近正態分佈,無論分佈的真實形狀如何。因此,我們知道拋硬幣是一個二元過程,用二項式分佈(正面或反面)來描述。
然而,如果我們考慮多次拋硬幣,得到任何特定的正面和反面組合的幾率就會開始不同。例如,如果我們拋硬幣十次,每次出現 5 次正面的幾率是最大的,但連續出現 10 次正面朝上的幾率是極其罕見的。想象一下拋硬幣 1,000 次,分佈接近正常的鐘形曲線。
什麼是 PDF 與 CDF?
概率密度函數 (PDF) 解釋了在任何給定時間或任何給定抽獎中哪些值可能出現在數據生成過程中。相反,累積分佈函數 (CDF) 描述了這些邊際概率如何相加,最終達到 100%(或 1.0)的可能結果。使用 CDF,我們可以看到變量的結果小於或等於某個預測值的可能性有多大。
結論
概率分佈函數 (PDF) 描述從樣本中抽取的隨機變量的期望值。 PDF 的形狀解釋了觀測值出現的可能性。
股票價格和回報往往遵循對數正態分佈而不是正態分佈,這表明相對於正態分佈的預測,下行損失比大幅上漲更常見。