什么是概率密度函数 (PDF)?
概率密度函数 (PDF) 是一种统计表达式,定义某些结果发生的概率。在此函数中,概率是数据集分布落在两个标准之间的百分比。
金融分析师使用 PDF 来了解回报如何分配,以评估投资价格和回报的风险和预期。
要点
- 概率密度函数是一种统计度量,用于衡量投资获得落在一定值范围内的回报的可能性并表明所涉及的风险。
- PDF 通常绘制在类似于钟形曲线的图表上,数据位于曲线下方。
- 两端的倾斜曲线表示风险/回报较大或较小。
了解概率密度函数 (PDF)
概率密度函数衡量投资回报落在指定范围内的频率。 PDF 通常用图表来描述,正常的钟形曲线表示中性市场风险,两端的倾斜曲线表示较高或较低的风险回报。
偏度是曲线较高部分向右或向左的偏移。如果曲线向左移动且右侧有长尾(右偏),分析师认为这表明存在更大的上行回报。如果它向右移动,长尾向左(左偏),分析师认为存在更大的下行风险。
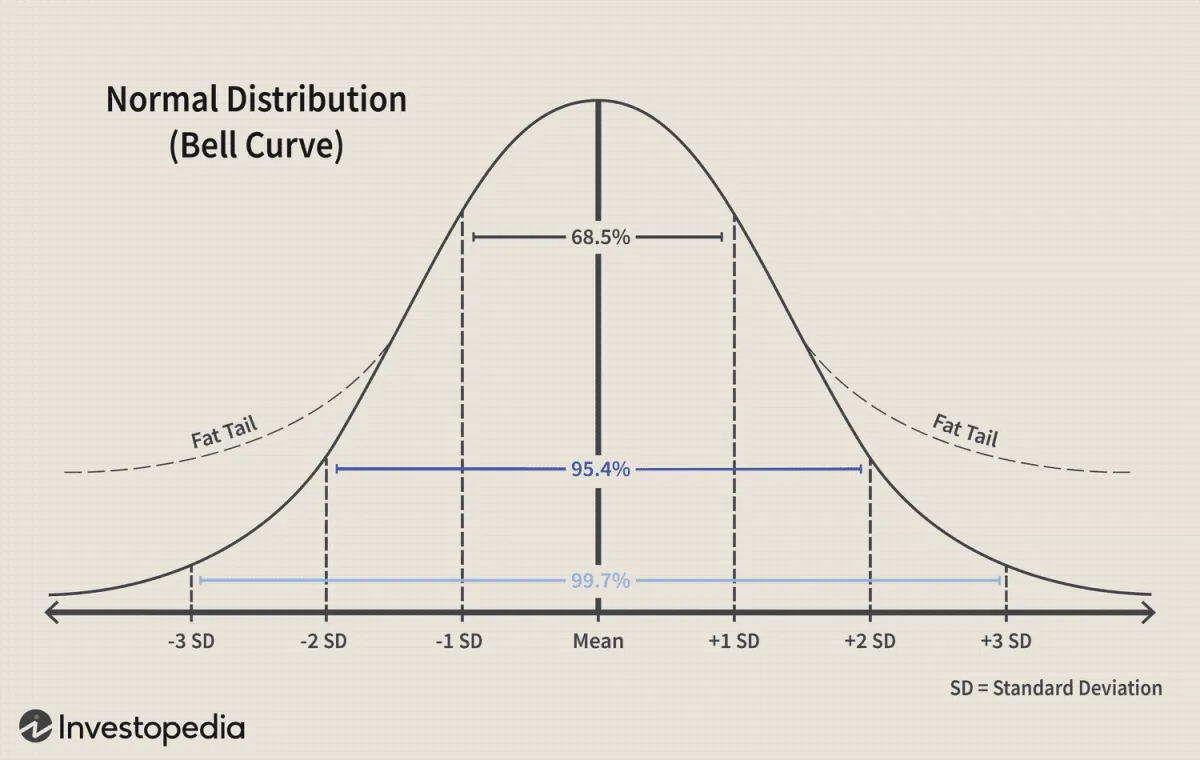
下图展示了具有钟形曲线的正态分布数据。数据平均值是中间的线,垂直线是标准差,或者数据偏离平均值的距离。
平均值两侧的前两条垂直线显示 68.5% 的数据落在平均值 +/-1 标准差范围内。因此,如果这是一条正态分布的股票收益曲线,您会发现 68.5% 的情况下,收益落在 -1 SD 和 +1 SD 线之间,并且市场风险是中性的(没有偏斜)。
您应该注意,投资回报很少(如果有的话)呈正态分布,因此图表可能永远不会是干净的正态分布曲线。
计算PDF
计算 PDF 并以图形方式绘制它可能涉及使用微分方程或积分的复杂计算。在实践中,需要图形计算器或统计软件包来计算概率密度函数。
概率密度函数的示例
概率密度函数衡量的是连续变量——股票和投资回报一般不是连续随机变量;它们是离散的。然而,大多数金融分析师假设回报和价格是连续的,以便他们可以对绩效进行建模并分析风险。
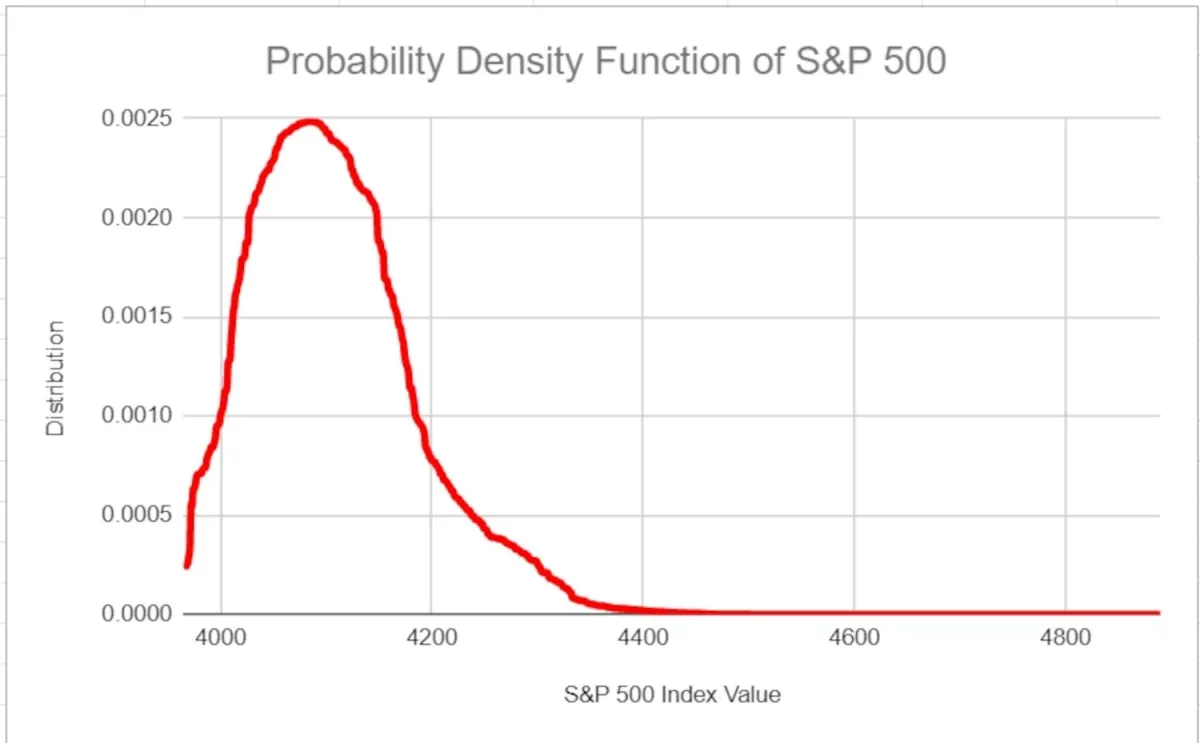
下图中,对 2020 年 5 月 20 日至 2023 年 5 月 19 日的标准普尔 500 指数值进行了排序和绘制。结果是一条右偏的钟形曲线,表明过去三年有可能获得更大的上行回报。
概率密度函数 (PDF) 告诉我们什么?
概率密度函数 (PDF) 描述了观察到数据生成过程产生的某些结果的可能性。 PDF 可以告诉我们哪些值最有可能出现,哪些值出现的可能性较小。这将根据 PDF 的形状和特征而变化。
什么是中心极限定理 (CLT) 以及它与 PDF 有何关系?
中心极限定理 (CLT)指出,随着样本量变大,样本中随机变量的分布将开始接近正态分布,无论分布的真实形状如何。因此,我们知道抛硬币是一个二元过程,用二项式分布(正面或反面)来描述。
然而,如果我们考虑多次抛硬币,得到任何特定的正面和反面组合的几率就会开始不同。例如,如果我们抛硬币十次,每次出现 5 次正面的几率是最大的,但连续出现 10 次正面朝上的几率是极其罕见的。想象一下抛硬币 1,000 次,分布接近正常的钟形曲线。
什么是 PDF 与 CDF?
概率密度函数 (PDF) 解释了在任何给定时间或任何给定抽奖中哪些值可能出现在数据生成过程中。相反,累积分布函数 (CDF) 描述了这些边际概率如何相加,最终达到 100%(或 1.0)的可能结果。使用 CDF,我们可以看到变量的结果小于或等于某个预测值的可能性有多大。
结论
概率分布函数 (PDF) 描述从样本中抽取的随机变量的期望值。 PDF 的形状解释了观测值出现的可能性。
股票价格和回报往往遵循对数正态分布而不是正态分布,这表明相对于正态分布的预测,下行损失比大幅上涨更常见。