什麼是 T 分佈?
t 分佈,也稱爲學生 t 分佈,是一種概率分佈,與正態分佈類似,呈鐘形,但尾部較粗。它用於估計小樣本量或未知方差的總體參數。與正態分佈相比,T 分佈出現極值的可能性更大,因此尾部較粗。
t分佈是統計學中計算t檢驗的基礎。
概要
- 當分母中使用估計標準差而不是真實標準差時,t 分佈是 z 分數的連續概率分佈。
- t 分佈與正態分佈類似,呈鐘形且對稱,但尾部較重,這意味着它往往會產生遠離平均值的值。
- T 檢驗在統計學中用於評估重要性。
T 分佈告訴您什麼?
尾部重量由 t 分佈的一個參數(稱爲自由度)決定,值越小,尾部越重,值越大,使 t 分佈更接近標準正態分佈,其平均值爲 0,標準差爲 1。
當從平均值爲 M、標準差爲 D 的正態分佈總體中抽取 n 個觀測值樣本時,由於樣本的隨機性,樣本平均值 m 和樣本標準差 d 將與 M 和 D 不同。
z 分數可以使用總體標準差計算爲 Z = (x - M)/D,該值具有均值爲 0、標準差爲 1 的正態分佈。但是,當使用估計的標準差時,t 分數計算爲 T = (m - M)/{d/sqrt(n)},d 和 D 之間的差異使分佈成爲自由度爲 (n - 1) 的 t 分佈,而不是均值爲 0、標準差爲 1 的正態分佈。
如何使用 T 分佈的示例
以下面的例子來說明 t 分佈在統計分析中的應用。首先,請記住,均值的置信區間是根據數據計算出的一系列數值,用於捕捉“總體”均值。這個區間是 m +- t*d/sqrt(n),其中 t 是 t 分佈中的一個臨界值。
例如,2001 年 9 月 11 日之前 27 個交易日內道瓊斯工業平均指數 (DJIA) 的平均回報率的 95% 置信區間爲 -0.33%,(+/- 2.055) * 1.07 / sqrt(27),得出 (持續) 平均回報率爲 -0.75% 至 +0.09% 之間的某個數字。2.055 是要調整的標準誤差量,是從 t 分佈中找到的。
由於 t 分佈比正態分佈具有更厚的尾部,因此它可以用作表現出過度峯度的金融回報模型,這將允許在這種情況下更現實地計算風險價值 (VaR) 。
T 分佈與正態分佈
當假設總體分佈爲正態分佈時,使用正態分佈。t 分佈與正態分佈類似,只是尾部更肥大。兩者都假設總體呈正態分佈。因此,t 分佈的峯度比正態分佈高。t 分佈獲得遠離平均值的值的概率比正態分佈大。
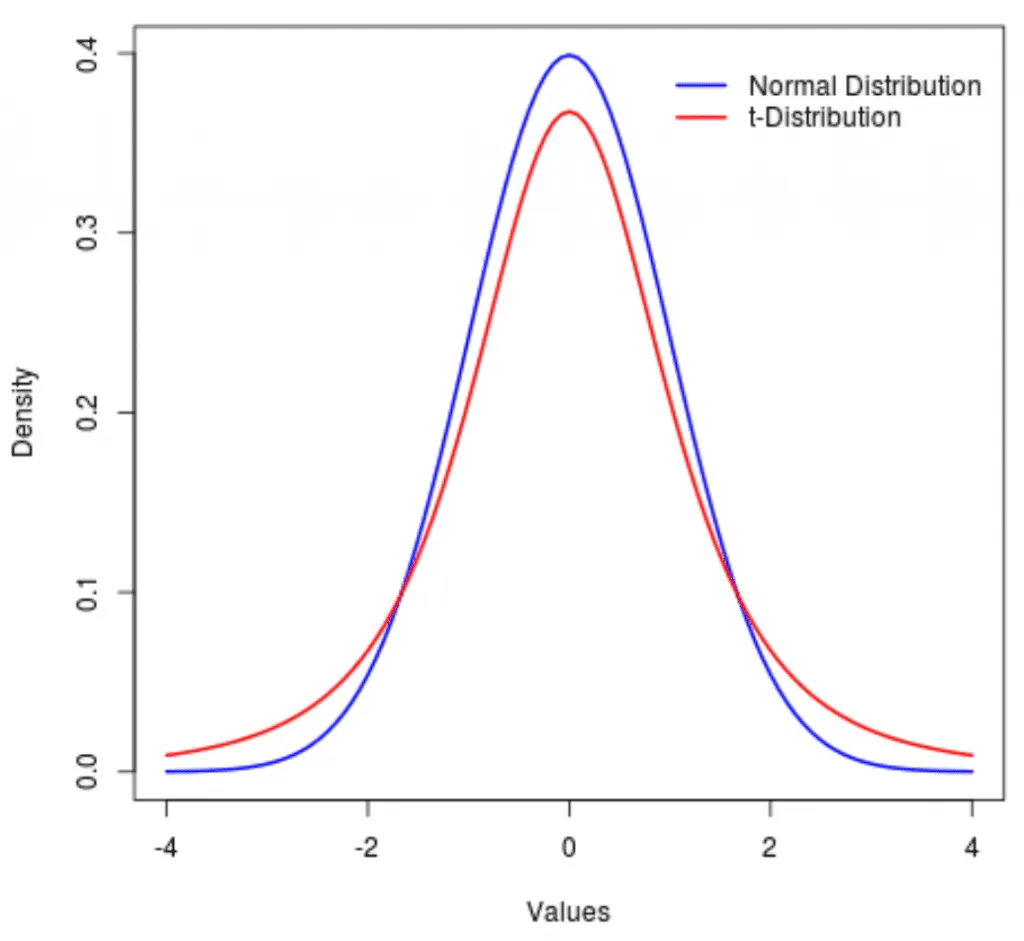
正態分佈與 t 分佈。
使用 T 分佈的侷限性
t 分佈相對於正態分佈可能會歪曲準確性。它的缺點僅在需要完美正態性時纔會出現。t 分佈只應在不知道總體標準差時使用。如果知道總體標準差並且樣本量足夠大,則應使用正態分佈以獲得更好的結果。
統計學中的 t 分佈是什麼?
t 分佈在統計學中用於估計小樣本量或不確定方差的總體參數。它也被稱爲學生 t 分佈。
何時應使用 t 分佈?
如果總體樣本量較小,且標準差未知,則應使用 t 分佈。如果不是,則應使用正態分佈。
正態分佈是什麼意思?
正態分佈是概率鐘形曲線的術語。它也被稱爲高斯分佈。
歸納總結
t 分佈在統計學中用於估計樣本量較小或未知變異的總體參數的重要性。與正態分佈一樣,t 分佈呈鐘形且對稱。與正態分佈不同的是,t 分佈的尾部較重,因此極值出現的可能性更大。