什么是 T 分布?
t 分布,也称为学生 t 分布,是一种概率分布,与正态分布类似,呈钟形,但尾部较粗。它用于估计小样本量或未知方差的总体参数。与正态分布相比,T 分布出现极值的可能性更大,因此尾部较粗。
t分布是统计学中计算t检验的基础。
要点
- 当分母中使用估计标准差而不是真实标准差时,t 分布是 z 分数的连续概率分布。
- t 分布与正态分布类似,呈钟形且对称,但尾部较重,这意味着它往往会产生远离平均值的值。
- T 检验在统计学中用于评估重要性。
T 分布告诉您什么?
尾部重量由 t 分布的一个参数(称为自由度)决定,值越小,尾部越重,值越大,使 t 分布更接近标准正态分布,其平均值为 0,标准差为 1。
当从平均值为 M、标准差为 D 的正态分布总体中抽取 n 个观测值样本时,由于样本的随机性,样本平均值 m 和样本标准差 d 将与 M 和 D 不同。
z 分数可以使用总体标准差计算为 Z = (x - M)/D,该值具有均值为 0、标准差为 1 的正态分布。但是,当使用估计的标准差时,t 分数计算为 T = (m - M)/{d/sqrt(n)},d 和 D 之间的差异使分布成为自由度为 (n - 1) 的 t 分布,而不是均值为 0、标准差为 1 的正态分布。
如何使用 T 分布的示例
以下面的例子来说明 t 分布在统计分析中的应用。首先,请记住,均值的置信区间是根据数据计算出的一系列数值,用于捕捉“总体”均值。这个区间是 m +- t*d/sqrt(n),其中 t 是 t 分布中的一个临界值。
例如,2001 年 9 月 11 日之前 27 个交易日内道琼斯工业平均指数 (DJIA) 的平均回报率的 95% 置信区间为 -0.33%,(+/- 2.055) * 1.07 / sqrt(27),得出 (持续) 平均回报率为 -0.75% 至 +0.09% 之间的某个数字。2.055 是要调整的标准误差量,是从 t 分布中找到的。
由于 t 分布比正态分布具有更厚的尾部,因此它可以用作表现出过度峰度的金融回报模型,这将允许在这种情况下更现实地计算风险价值 (VaR) 。
T 分布与正态分布
当假设总体分布为正态分布时,使用正态分布。t 分布与正态分布类似,只是尾部更肥大。两者都假设总体呈正态分布。因此,t 分布的峰度比正态分布高。t 分布获得远离平均值的值的概率比正态分布大。
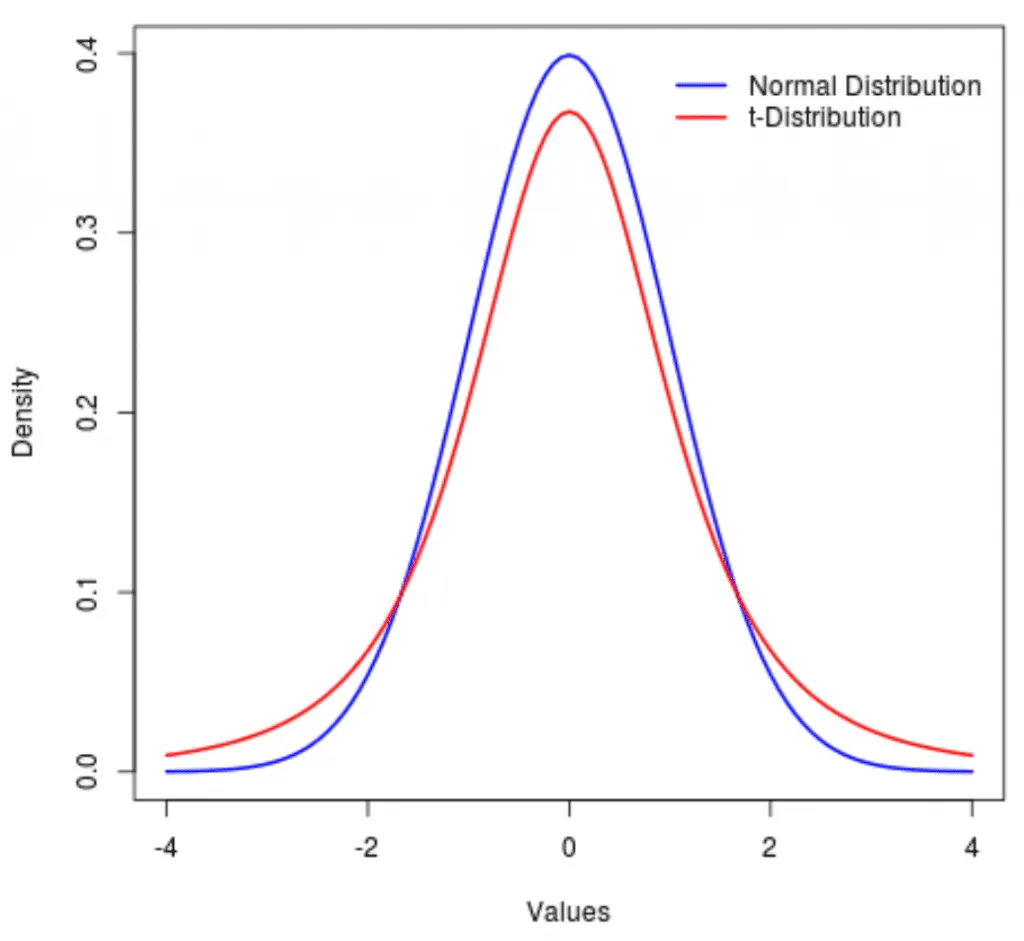
正态分布与 t 分布。
使用 T 分布的局限性
t 分布相对于正态分布可能会歪曲准确性。它的缺点仅在需要完美正态性时才会出现。t 分布只应在不知道总体标准差时使用。如果知道总体标准差并且样本量足够大,则应使用正态分布以获得更好的结果。
统计学中的 t 分布是什么?
t 分布在统计学中用于估计小样本量或不确定方差的总体参数。它也被称为学生 t 分布。
何时应使用 t 分布?
如果总体样本量较小,且标准差未知,则应使用 t 分布。如果不是,则应使用正态分布。
正态分布是什么意思?
正态分布是概率钟形曲线的术语。它也被称为高斯分布。
结论
t 分布在统计学中用于估计样本量较小或未知变异的总体参数的重要性。与正态分布一样,t 分布呈钟形且对称。与正态分布不同的是,t 分布的尾部较重,因此极值出现的可能性更大。