什麼是概率分佈?
概率分佈是一種統計函數,描述隨機變量在給定範圍內可能取的所有可能值和可能性。該範圍將限制在最小和最大可能值之間,但可能值可能繪製在概率分佈上的精確位置取決於許多因素。這些因素包括分佈的平均值、標準差、偏度和峯度。
概率分佈如何運作
也許最常見的概率分佈是正態分佈或“鐘形曲線”,儘管存在幾種常用的分佈。通常,某些現象的數據生成過程將決定其概率分佈。這個過程稱爲概率密度函數。
概率分佈還可用於創建累積分佈函數 (CDF),該函數累積出現的概率,並且始終從 0 開始到 100% 結束。
學者、金融分析師和基金經理等可以確定特定股票的概率分佈,以評估該股票未來可能產生的預期回報。股票的回報歷史可以從任何時間間隔進行衡量,但很可能只包含股票回報的一小部分,這將使分析受到抽樣誤差的影響。通過增加樣本量,可以顯着減少該誤差。
要點
- 概率分佈描述了給定數據生成過程的可能值的預期結果。
- 概率分佈有多種形狀,具有不同的特徵,如均值、標準差、偏度和峯度所定義。
- 投資者使用概率分佈來預測股票等資產隨着時間的推移的回報並對沖風險。
概率分佈的類型
概率分佈有許多不同的分類。其中一些包括正態分佈、卡方分佈、二項分佈和泊松分佈。不同的概率分佈服務於不同的目的並代表不同的數據生成過程。例如,二項式分佈評估在給定次數的試驗中事件多次發生的概率,並給出每次試驗中事件的概率。可以通過記錄籃球運動員在一場比賽中罰球的次數來生成,其中 1 = 投籃,0 = 投失。另一個典型的例子是使用一枚均勻的硬幣,並計算出該硬幣連續拋 10 次後正面朝上的概率。二項式分佈是離散的,而不是連續的,因爲只有 1 或 0 是有效響應。
最常用的分佈是正態分佈,常用於金融、投資、科學和工程。正態分佈完全由其均值和標準差來表徵,這意味着分佈沒有偏斜並且確實表現出峯度。這使得分佈對稱,並且在繪製時被描繪爲鐘形曲線。正態分佈的定義是均值(平均值)爲零,標準差爲 1.0,偏斜爲零,峯度 = 3。在正態分佈中,大約 68% 收集的數據將落在 +/- 1 個標準範圍內平均值的偏差;大約 95% 在 +/- 兩個標準偏差內; 99.7% 在三個標準差之內。與二項分佈不同,正態分佈是連續的,這意味着所有可能的值都被表示(而不是隻有 0 和 1,中間沒有任何值)。
投資中使用的概率分佈
股票收益通常被認爲是正態分佈的,但實際上,它們表現出峯度,具有較大的負收益和正收益,似乎比正態分佈預測的要多。事實上,由於股票價格的界限爲零,但具有潛在的無限上漲空間,股票回報的分佈被描述爲對數正態分佈。這顯示在股票收益圖上,分佈的尾部具有更大的厚度。
概率分佈也經常用於風險管理,並根據歷史收益的分佈來評估投資組合發生損失的概率和金額。投資中使用的一種流行的風險管理指標是風險價值(VaR)。 VaR 產生給定投資組合的概率和時間範圍內可能發生的最小損失。或者,投資者可以使用 VaR 獲得一定損失金額和時間範圍內的損失概率。濫用和過度依賴VaR被認爲是 2008 年金融危機的主要原因之一。
概率分佈的示例
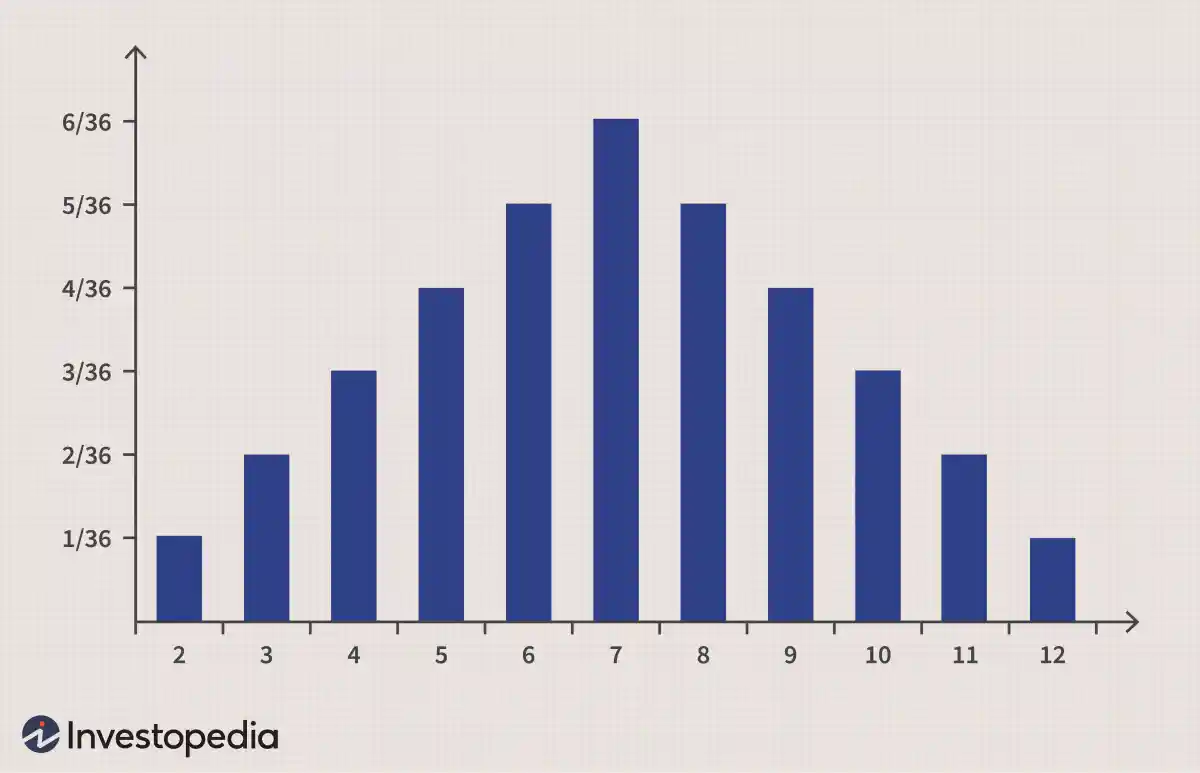
作爲概率分佈的一個簡單示例,讓我們看一下擲兩個標準六面骰子時觀察到的數字。每個骰子都有 1/6 的概率滾動任何單個數字(1 到 6),但兩個骰子的總和將形成下圖所示的概率分佈。七是最常見的結果(1+6、6+1、5+2、2+5、3+4、4+3)。另一方面,二和十二的可能性要小得多(1+1 和 6+6)。