L系統
就分形的計算機實現來說,有很多不同的算法,但是具體哪種算法更有效、更實用則要針對不同的情況。分形的描述常用的方法有L系統和IFS系統兩種。從它們所繪製出的分形來說,L系統要比IFS系統簡單。L系統只是簡單的字符串的迭代,而IFS系統在這方面要複雜得多,如Julia集等。
林氏系統(通常稱L系統)是林德梅葉1968年爲模擬生物形態而設計的,後來史密斯於1984年、普魯辛凱維奇於1986年,分別將它應用於計算機圖形學,引起生物學界和計算機界人士極大興趣,一時發表了許多論文和專著。
L系統基本原理
L系統實際上是字符串重寫系統,L系統的工作原理非常簡單。如果把一個字符看做是一種操作,而且每種不同的字符解釋成不同的操作。基於這種思想,那麼就可以利用字符串生成各種不同的分形圖形,於是只要能生成字符串,也就等於生成了圖形。
L系統中生成圖形的字符串可以是由任意的可識別的字符組成的,如“F"“-”、“+”。在程序設計中,“F”表示從當前位置向前一個單位長度,同時畫線;“-”表示從當前方向順時針旋轉一個給定的角度;“+”表示從當前方向逆時針旋轉一個給定的角度。在生成字符串的過程中,先從一個稱爲公理的起始字符開始,再將該公理字符替換成規則中的子字符串,這是第一次迭代。然後,把子字符串作爲母串,將母串中的字符用規則中的子串替代,依次類推,就可以完成L系統的迭代,其字符串的長度由迭代次數控制。
隨機L系統
自然界中的物質形態不是固定不變的,而是隨機的,儘管它們有一定的規律可尋。世界上沒有完全按相同方式生長的兩棵植物,即使是同一種植物,其形態也存在很大差別,如莖的高矮、開花的位置、種子的形狀等,尤其是由環境的影響帶來的形態變異。
例如,作物由於肥料充足而粒大穗多。基於此,從模擬植物的效果來說,用上述方法得到的圖形顯然有些呆板,不那麼形象了.如果在保留某種植物主要特徵的情況下,爲了產生細節上的不同變化,以求生成的植物圖形更加生動逼真,那麼可以引入隨機性,它的好處就是模擬出來的植物更加接近真實的事物形態。隨機的L系統是有序的四元素集,其表達式爲:
G=<V,ω,P,π>
其中V,ω的意義和三元式相同,然而這裏的P卻是隨機的生成規則集,π爲函數,且有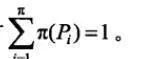
L系統的算法
L系統側重於植物拓撲結構的表達,它試圖用抽象出來的規則描述植物的形態及生長規律,該系統具有定義簡潔、結構化程度高、易於實現等優點。通常計算機生成分形圖形的算法大多是所謂的迭代,在程序中的實現形式是遞歸調用。衆所周知,遞歸程序與非遞歸程序的區別在於:遞歸程序很難用通常的方法來控制它的流程。雖然這一點是一個問題,但是這也是它的優點之所在,因爲它的算法非常簡單。正是基於遞歸算法的這一優點,在編制L系統程序的時候就是採用這種算法。