L系统
就分形的计算机实现来说,有很多不同的算法,但是具体哪种算法更有效、更实用则要针对不同的情况。分形的描述常用的方法有L系统和IFS系统两种。从它们所绘制出的分形来说,L系统要比IFS系统简单。L系统只是简单的字符串的迭代,而IFS系统在这方面要复杂得多,如Julia集等。
林氏系统(通常称L系统)是林德梅叶1968年为模拟生物形态而设计的,后来史密斯于1984年、普鲁辛凯维奇于1986年,分别将它应用于计算机图形学,引起生物学界和计算机界人士极大兴趣,一时发表了许多论文和专著。
L系统基本原理
L系统实际上是字符串重写系统,L系统的工作原理非常简单。如果把一个字符看做是一种操作,而且每种不同的字符解释成不同的操作。基于这种思想,那么就可以利用字符串生成各种不同的分形图形,于是只要能生成字符串,也就等于生成了图形。
L系统中生成图形的字符串可以是由任意的可识别的字符组成的,如“F"“-”、“+”。在程序设计中,“F”表示从当前位置向前一个单位长度,同时画线;“-”表示从当前方向顺时针旋转一个给定的角度;“+”表示从当前方向逆时针旋转一个给定的角度。在生成字符串的过程中,先从一个称为公理的起始字符开始,再将该公理字符替换成规则中的子字符串,这是第一次迭代。然后,把子字符串作为母串,将母串中的字符用规则中的子串替代,依次类推,就可以完成L系统的迭代,其字符串的长度由迭代次数控制。
随机L系统
自然界中的物质形态不是固定不变的,而是随机的,尽管它们有一定的规律可寻。世界上没有完全按相同方式生长的两棵植物,即使是同一种植物,其形态也存在很大差别,如茎的高矮、开花的位置、种子的形状等,尤其是由环境的影响带来的形态变异。
例如,作物由于肥料充足而粒大穗多。基于此,从模拟植物的效果来说,用上述方法得到的图形显然有些呆板,不那么形象了.如果在保留某种植物主要特征的情况下,为了产生细节上的不同变化,以求生成的植物图形更加生动逼真,那么可以引入随机性,它的好处就是模拟出来的植物更加接近真实的事物形态。随机的L系统是有序的四元素集,其表达式为:
G=<V,ω,P,π>
其中V,ω的意义和三元式相同,然而这里的P却是随机的生成规则集,π为函数,且有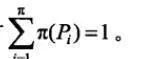
L系统的算法
L系统侧重于植物拓扑结构的表达,它试图用抽象出来的规则描述植物的形态及生长规律,该系统具有定义简洁、结构化程度高、易于实现等优点。通常计算机生成分形图形的算法大多是所谓的迭代,在程序中的实现形式是递归调用。众所周知,递归程序与非递归程序的区别在于:递归程序很难用通常的方法来控制它的流程。虽然这一点是一个问题,但是这也是它的优点之所在,因为它的算法非常简单。正是基于递归算法的这一优点,在编制L系统程序的时候就是采用这种算法。