缠论第65课:再说分型,笔和线段
本ID反复强调,本ID理论的关键是一套几何化的思维,因此你需要从最基本的定义出发。这一点在实际操作的辨认中更为重要。所有复杂的情况,其实从最基本的定义出发,都没有任何困难可言。
例如对于分型,其中最大的麻烦,就是所谓的前后K线之间的包含关系。其次,有点简单的几何思维,根据定义,任何人都可以马上得出以下一些推论。
1.用[di,gi]代表第i根K线的最低点和最高点构成的区间。当向上时,顺次n个具有包含关系的K线组,等价于[maxdi,maxgi]的区间对应的K线。也就是说,这n个K线,和最低最高区间为[maxdi,maxgi]的K线是一回事情。向下时,顺次n个包含关系的K线组,等价于[mindi,mingi]的区间对应的K线。
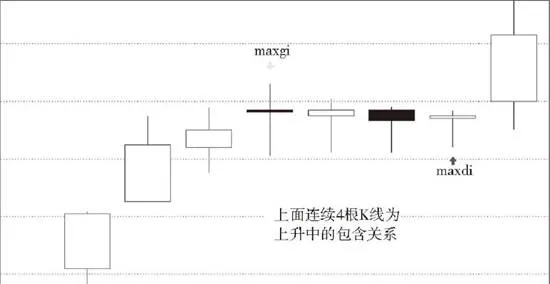
上图所示为上升中的包含关系示意图
2.结合律是本ID理论中最基础的定律,在K线的包含关系处理中,当然也需要遵守。但包含关系不符合传递律,也就是说,第1根、第2根K线是包含关系,第2根、第3根也是包含关系,但并不意味着第1根、第3根就有包含关系。因此在K线包含关系的分析中,还要遵守顺序原则,就是先用第1根、第2根K线的包含关系确认新的K线,然后用新的K线去和第3根比较。如果有包含关系,继续用包含关系的合并法则结合成新的K线;如果没有,就按正常K线处理。
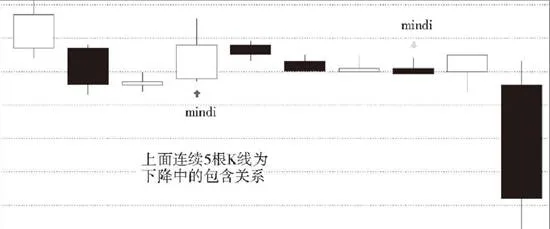
上图所示为下降中的包含关系示意图
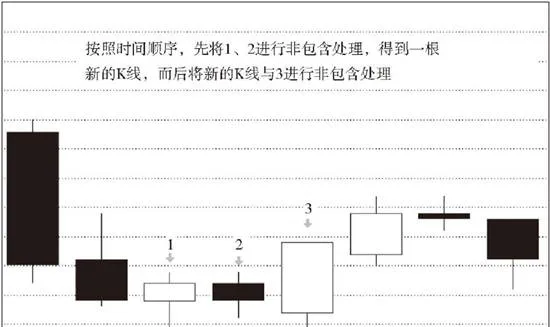
上图所示为顺序处理包含关系示意图
3.有人可能还要问,什么是向上?什么是向下?其实这根本没什么可说的,任何看过图的人都知道什么是向上,什么是向下。当然,本ID的理论是严格的几何理论,对向上向下,也可以严格地定义。
假设第n根K线满足第n根与第n+1根的包含关系,而第n根与第n-1根不是包含关系,那么如果gn≥gn-1,那么称第n-l、n、n+1根K线是向上的;如果dn≤dn-1,那么称第n-1. n、n+1根K线是向下的。
有人可能又要问,如果gn<gn-1且dn>dn-1,这算什么?那就是一种包含关系,就违反了前面第n根与第n-1根不是包含关系的假设。同样道理,gn≥gn-1与dn≤dn-1不可能同时成立。
上面包含关系的定义已经十分清楚,都是一些最精确的几何定义。只要按照定义来做,没有任何图是不可以精确无误地、按统一的标准去找出所有的分型来的。
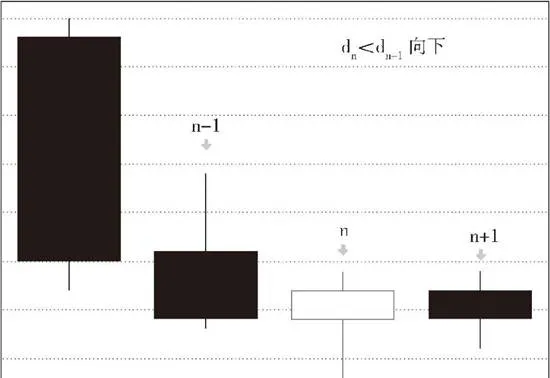
上图是第n-n、n+1根K线向下关系示意图
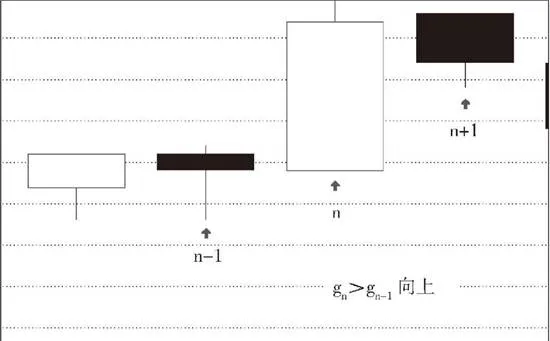
上图是第n-n、n+1根K线向上关系示意图
注意,这种定义是唯一的,有统一答案的。就算是本ID如果弄错了,那也是错,没有任何含糊的地方。这个答案与时间无关,与人无关,是客观的,不可更改的,唯一的要求就是被分析的K线已经走出来。
从这里可以看出,本ID理论的当下性也就有了一个很客观的描述。为什么要当下的?因为如果当下那些K线还有没走出来,那么具体的分型就找不出来,相应的笔、线段、最低级别中枢、高级别走势类型等就不可能划分出来,这样就无从分析了。
一旦当下的K线走出来,就可以当下按客观标准唯一地找出相应的分型结构。当下的分析和事后的分析是一样的,分析的结果也是一样的,没有任何的不同。因此当下性就是本ID的客观性。
有人可能要问,如果看30分钟图,K线可能会一直犬牙交错,找不到分型。这有什么奇怪的?在年线图里,找到分型的机会更小,十几年找不到一个也很正常,这里还是用显微镜倍数来比喻问题。
确定显微镜的倍数,就按看到的K线用定义严格地寻找。没有符合定义的对象,就是确实不存在,就这么简单。如果希望能分析得更精确,那就用小级别的图,这样自然能分辨得更清楚。
再次强调,用什么图与以什么级别操作没有任何必然联系。用1分钟图,也可以找出年线级别的背驰,然后进行相应级别的操作。看1分钟图,并不意味着一定要玩超短线。把显微镜当成显微镜观察的对象,肯定是不对的。
从分型到笔,必须是一顶一底相连接。那么两个顶或底能构成一笔吗?这里分两种情况。
第一种,在两个顶或底中间有其他的顶和底。这种情况下,只是把好几笔当成了一笔,只要继续用一顶一底的原则处理,自然可以解决。
第二种,在两个顶或底中间没有其他的顶和底。这种情况意味着第一个顶或底后的转折级别太小,不足以构成值得考察的对象。这种情况下,第一个顶或底可以忽略不计。
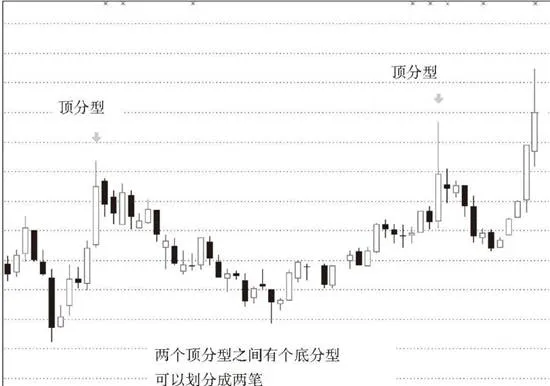
上图所示为情况示意图
根据上面的分析,对第二种情况进行相应处理之后,可以严格地说,先顶后底,构成向下一笔;先底后顶,构成向上一笔。所有的图形,都可以唯一地分解为上下交替的笔的连接。
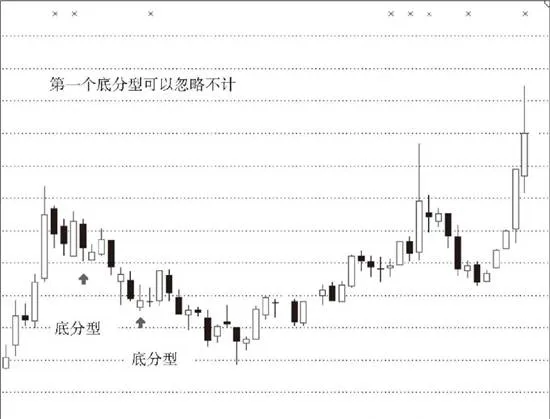
上图所示为情况示意图
显然,除了第二种情况中的第一个顶或底类似的分型,其他类型的分型,都唯一地分别属于相邻的上下两笔,是这两笔间的连接。用一个最简单的比喻,膝盖就是分型,而大腿和小腿就是连接的两笔。
有了笔,那么线段就很简单了。线段至少有3笔。线段无非有两种,从向上一笔开始的线段和从向下一笔开始的线段。
对于从向上一笔开始的,其中的分型构成这样的序列:d1g1,d2g2,d3g3…dngn(其中di代表第i个底,gi代表第i个顶)。如果找到i和j,j≥i+2,使得dj≤gi,那么称向上线段被笔破坏。
对于从向下一笔开始的,其中的分型构成这样的序列:g1d1,g2d2…gndn(其中di代表第i个底,gi代表第i个顶)。如果找到i和j,j≥i+2,使得gj≥di,那么称向下线段被笔破坏。
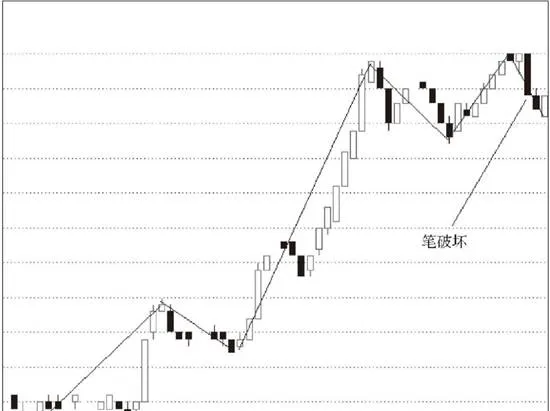
上图所示为向上线段被笔破坏示意图
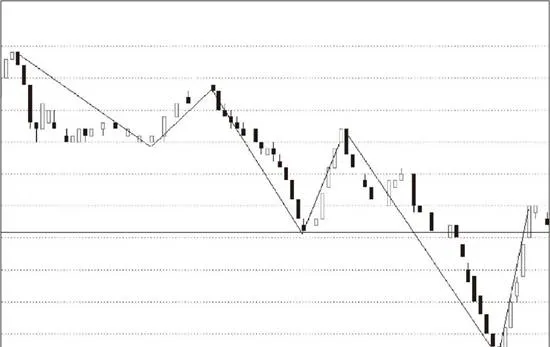
上图所示为向下线段被笔破坏示意图
线段有一个最基本的前提,就是线段的前3笔必须有重叠的部分,这个前提在前面可能没有特别强调,这里必须特别强调一次。线段至少有3笔,但并不是连续的3笔就一定构成线段,这3笔必须有重叠的部分。
由上面线段被笔破坏的定义,可以证明缠中说禅线段分解定理:线段被破坏,当且仅当至少被有重叠部分的连续3笔的其中一笔破坏。只要构成有重叠部分的前3笔,那么必然会形成一段线段。换言之,线段破坏的充要条件,就是被另一个线段破坏。
以上都是些最严格的几何定义。真想把问题搞清楚的人,请自己根据定义多画图,或者对照真实的走势图用定义多分析。注意,所有分析答案,只和你看的走势品种与级别图有关。在客观地观照对象与显微镜倍数确定的情况下,任何分析都是唯一的,客观的,不以任何人的意志为转移。
如果分型、笔、线段这些最基础的东西都没有搞清楚,不能做到在任何时刻,面对任何最复杂的图形,当下地进行快速正确的分解,就说要掌握本ID的理论,那纯粹是瞎掰。
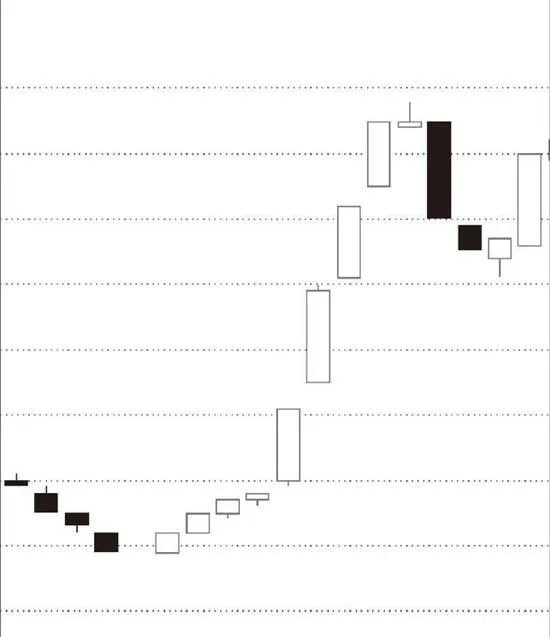
上图中连续3笔没有重叠,不构成线段
缠论点睛
1.一笔中间的分型,可以称作中继分型。如果一个分型之后的反向力度很弱,那么该分型就有可能演化为中继分型。
2.线段的前3笔必须有重叠,且第一笔和最后一笔的方向一致。也就是说线段中,笔的个数都是奇数且为大于或等于3的奇数。
投资微言
低级别图上用中枢、走势类型,高级别图上用分型、笔、线段,等于有两套有用的工具去分析同一走势,这是天大的好事。