金融機構和企業以及個人投資者和研究人員經常使用金融時間序列數據(例如資產價格、匯率、 GDP 、通貨膨脹和其他宏觀經濟指標)進行經濟預測、股票市場分析或數據本身的研究。
但細化數據是將其應用於股票分析的關鍵。在本文中,我們將向您展示如何隔離與您的股票報告相關的數據點。
概要
- 在統計學中,時間序列分析涉及測量事物相對於某些感興趣的變量隨時間的變化情況。
- 當時間序列平穩時,這意味着數據的某些屬性不會隨時間而改變。
- 然而,一些時間序列是非平穩的,即變量之間的值和關聯會隨着時間而變化。
- 在金融領域,許多過程都是非平穩的,因此必須適當處理。
非平穩時間序列數據
數據點通常是非平穩的,或者具有隨時間變化的均值、方差和協方差。非平穩行爲可以是趨勢、週期、隨機遊走或三者的組合。
非平穩數據通常是不可預測的,無法建模或預測。使用非平穩時間序列獲得的結果可能是虛假的,因爲它們可能表明兩個變量之間存在關係,而實際上不存在關係。爲了獲得一致、可靠的結果,需要將非平穩數據轉換爲平穩數據。
與非平穩過程相比,非平穩過程具有可變的方差和不會保持在接近或隨時間返回到長期均值的位置,而平穩過程則圍繞恆定的長期均值迴歸,並且具有與時間無關的恆定方差。
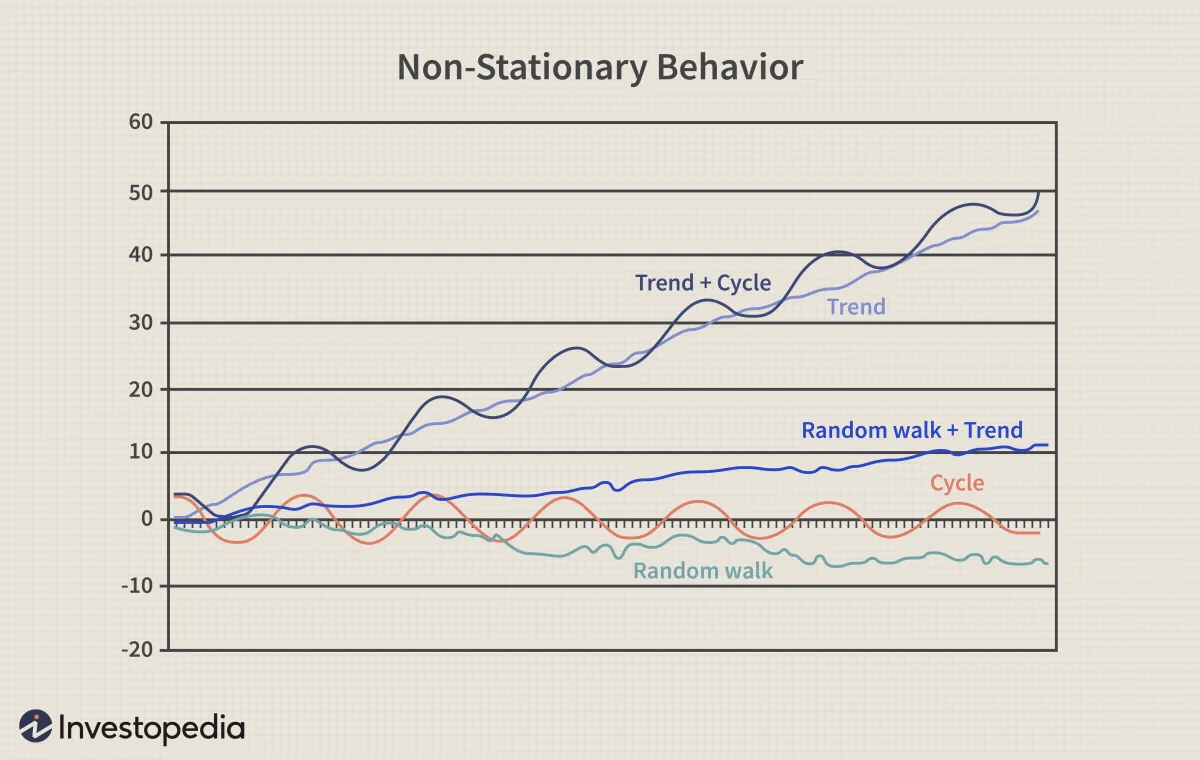
非平穩過程的類型
在討論非平穩金融時間序列數據的變換之前,我們應該區分不同類型的非平穩過程。這將使我們更好地理解這些過程,並使我們能夠應用正確的變換。
非平穩過程的例子是有或沒有漂移的隨機遊動(緩慢穩定的變化)和確定性趨勢(在整個系列的生命週期中,趨勢是恆定的、正的或負的,與時間無關)。
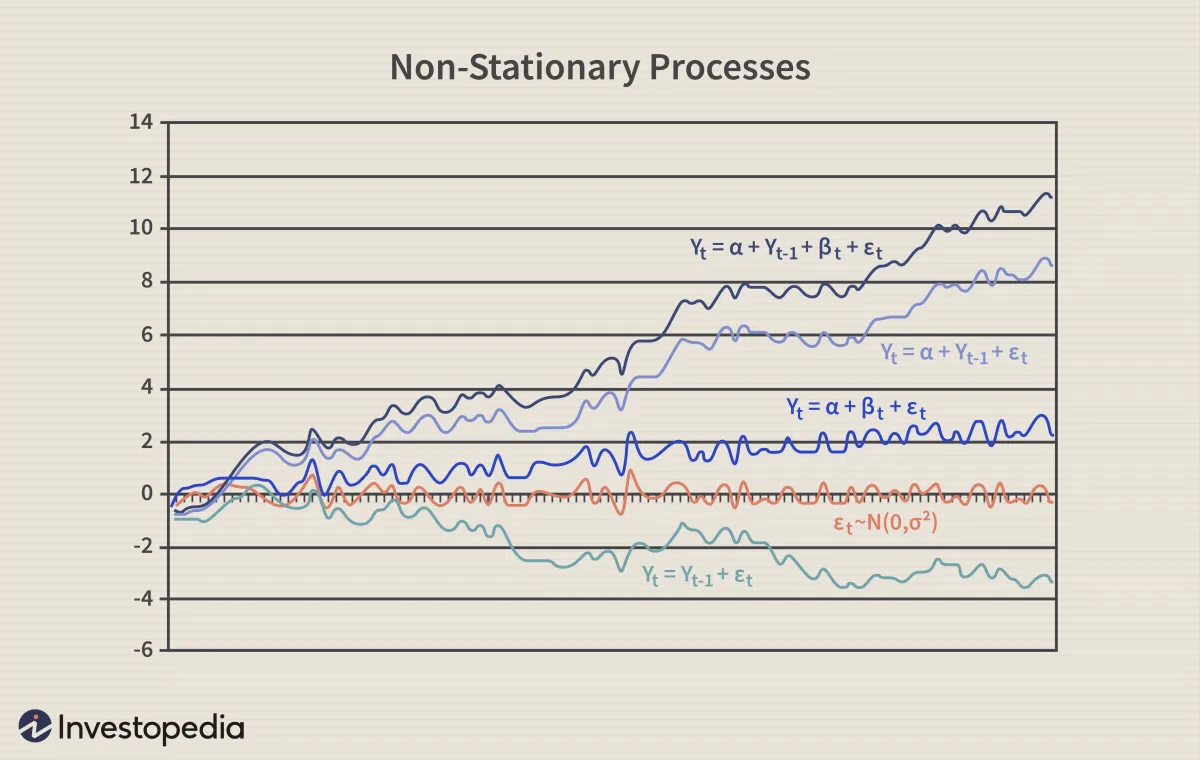
- 純隨機遊走 (Y t = Y t-1 + ε t )隨機遊走預測時間“t”的值將等於上一週期值加上隨機(非系統)分量,該分量是白噪聲,這意味着 ε t是獨立且相同分佈的,均值爲“0”,方差爲“σ²”。隨機遊走也可以稱爲某種階數的積分過程、具有單位根的過程或具有隨機趨勢的過程。它是一個非均值迴歸過程,可以正向或負向偏離均值。隨機遊走的另一個特徵是方差隨時間變化,並隨着時間趨於無窮大;因此,隨機遊走無法預測。
- 帶漂移的隨機遊走(Y t = α + Y t-1 + ε t )如果隨機遊走模型預測時間“t”的值將等於上一週期的值加上一個常數或漂移 (α) 和一個白噪聲項 (ε t ),則該過程爲帶漂移的隨機遊走。它也不會恢復到長期平均值,並且具有隨時間變化的方差。
- 確定性趨勢 (Y t = α + βt + ε t )帶有漂移的隨機遊走經常與確定性趨勢混淆。兩者都包括漂移和白噪聲成分,但在隨機遊走的情況下,時間“t”的值迴歸於上一週期的值 (Y t-1 ),而在確定性趨勢的情況下,它迴歸於時間趨勢 (βt)。具有確定性趨勢的非平穩過程的平均值圍繞固定趨勢增長,該趨勢是恆定的並且與時間無關。
- 具有漂移和確定性趨勢的隨機遊走 (Y t = α + Y t-1 + βt + ε t )另一個示例是將隨機遊走與漂移分量 (α) 和確定性趨勢 (βt) 相結合的非平穩過程。它通過上一週期的值、漂移、趨勢和隨機分量來指定時間“t”的值。
趨勢和差異平穩
有或無漂移的隨機遊動都可以通過差分(從 Y t 中減去 Y t-1 ,取差分 Y t - Y t-1 )轉換爲平穩過程,對應於 Y t - Y t-1 = ε t或 Y t - Y t-1 = α + ε t ,然後該過程變爲差分平穩。差分的缺點是每次取差分時,該過程都會丟失一個觀測值。
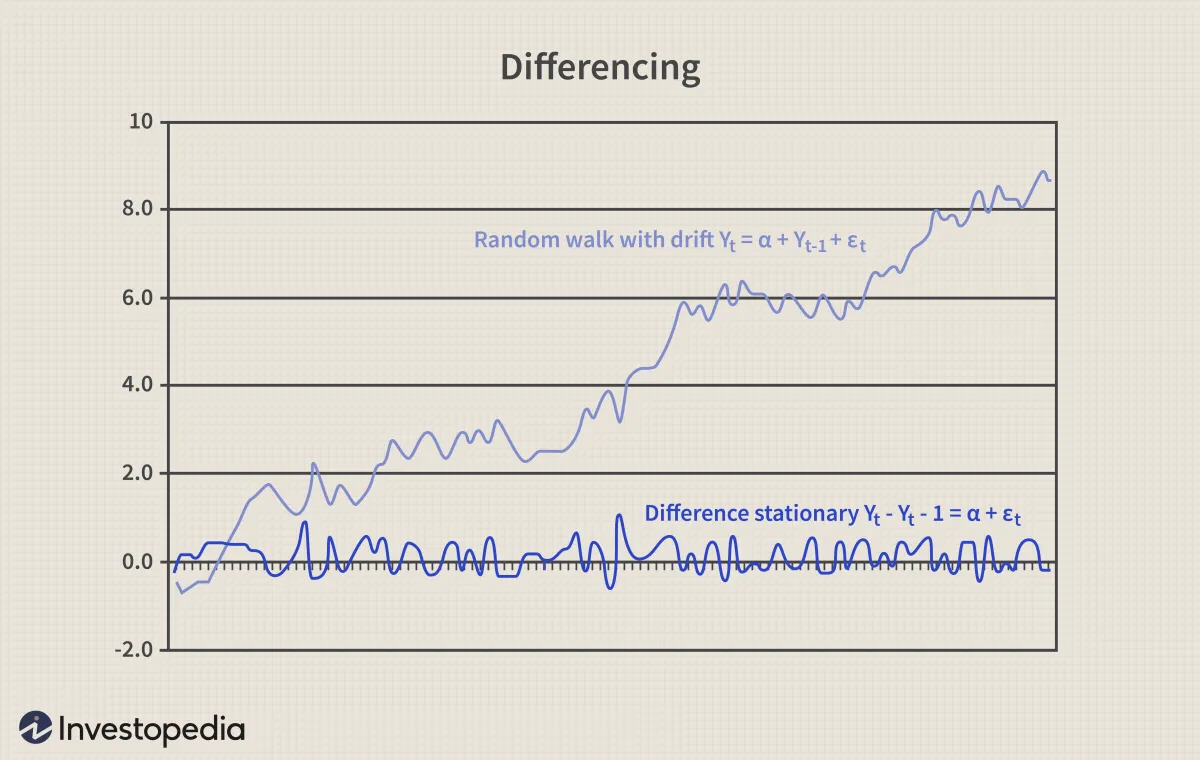
具有確定性趨勢的非平穩過程在消除趨勢(或去趨勢)後變爲平穩過程。例如,通過減去趨勢 βt,Yt = α + βt + εt 可轉換爲平穩過程:Yt - βt = α + εt,如下圖所示。當使用去趨勢將非平穩過程轉換爲平穩過程時,不會丟失任何觀察值。
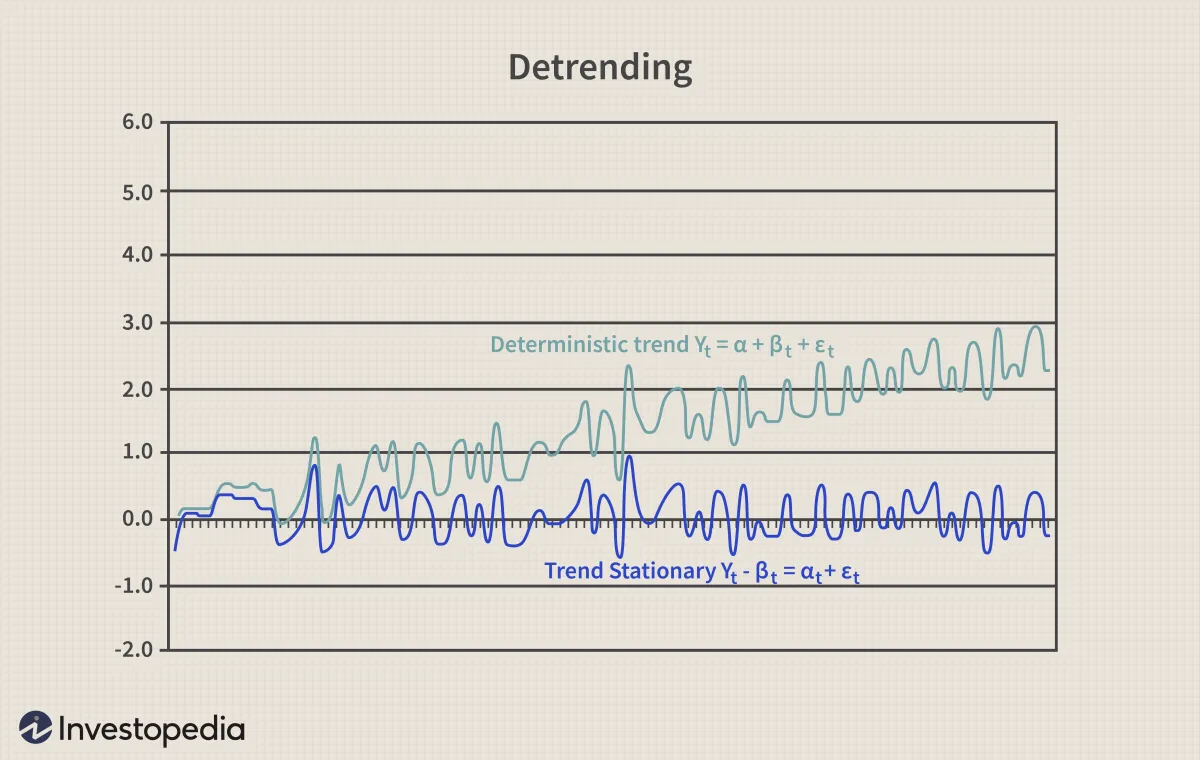
對於具有漂移和確定性趨勢的隨機遊走,去趨勢可以消除確定性趨勢和漂移,但方差將繼續趨於無窮大。因此,還必須應用差分來消除隨機趨勢。
綜述
在金融模型中使用非平穩時間序列數據會產生不可靠和虛假的結果,並導致理解和預測不佳。解決該問題的方法是轉換時間序列數據,使其變爲平穩的。如果非平穩過程是有或無漂移的隨機遊走,則通過差分將其轉換爲平穩過程。另一方面,如果所分析的時間序列數據表現出確定性趨勢,則可以通過去趨勢來避免虛假結果。
有時非平穩序列可能同時結合隨機趨勢和確定性趨勢,爲了避免獲得誤導性結果,應該同時應用差分和去趨勢,因爲差分將消除方差中的趨勢,而去趨勢將消除確定性趨勢。