金融机构和企业以及个人投资者和研究人员经常使用金融时间序列数据(例如资产价格、汇率、 GDP 、通货膨胀和其他宏观经济指标)进行经济预测、股票市场分析或数据本身的研究。
但细化数据是将其应用于股票分析的关键。在本文中,我们将向您展示如何隔离与您的股票报告相关的数据点。
摘要
- 在统计学中,时间序列分析涉及测量事物相对于某些感兴趣的变量随时间的变化情况。
- 当时间序列平稳时,这意味着数据的某些属性不会随时间而改变。
- 然而,一些时间序列是非平稳的,即变量之间的值和关联会随着时间而变化。
- 在金融领域,许多过程都是非平稳的,因此必须适当处理。
非平稳时间序列数据
数据点通常是非平稳的,或者具有随时间变化的均值、方差和协方差。非平稳行为可以是趋势、周期、随机游走或三者的组合。
非平稳数据通常是不可预测的,无法建模或预测。使用非平稳时间序列获得的结果可能是虚假的,因为它们可能表明两个变量之间存在关系,而实际上不存在关系。为了获得一致、可靠的结果,需要将非平稳数据转换为平稳数据。
与非平稳过程相比,非平稳过程具有可变的方差和不会保持在接近或随时间返回到长期均值的位置,而平稳过程则围绕恒定的长期均值回归,并且具有与时间无关的恒定方差。
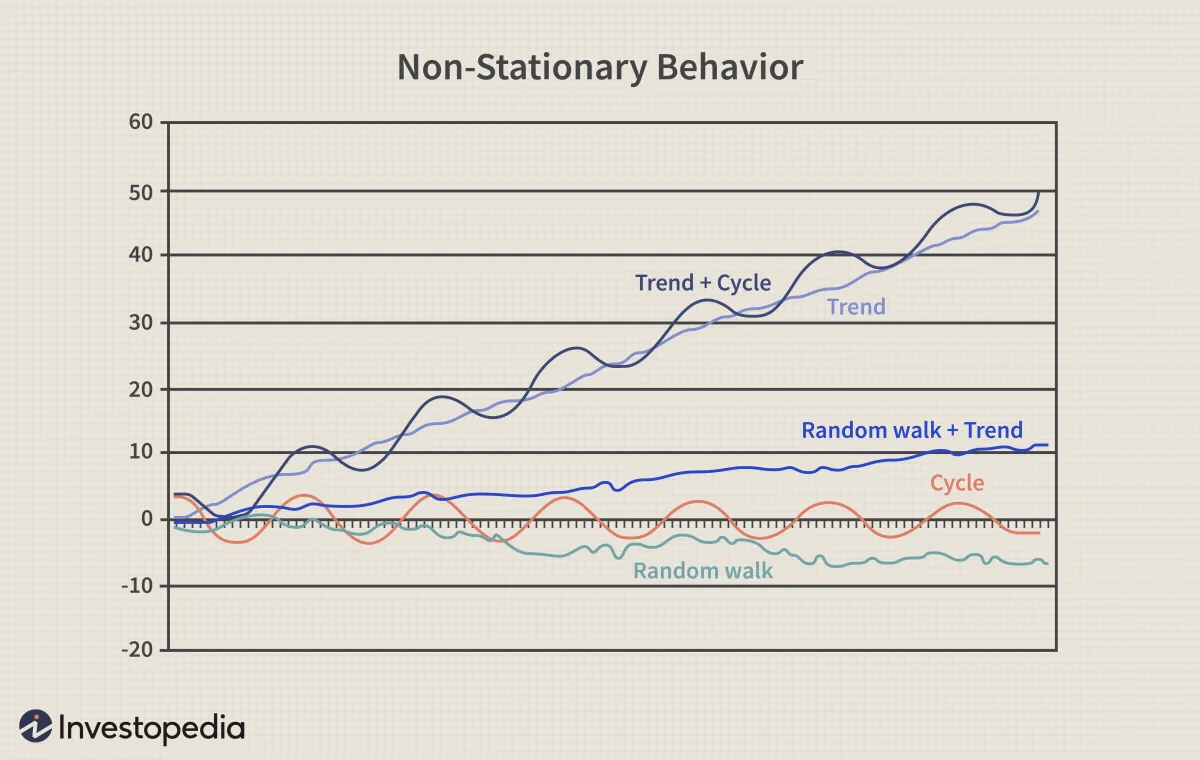
非平稳过程的类型
在讨论非平稳金融时间序列数据的变换之前,我们应该区分不同类型的非平稳过程。这将使我们更好地理解这些过程,并使我们能够应用正确的变换。
非平稳过程的例子是有或没有漂移的随机游动(缓慢稳定的变化)和确定性趋势(在整个系列的生命周期中,趋势是恒定的、正的或负的,与时间无关)。
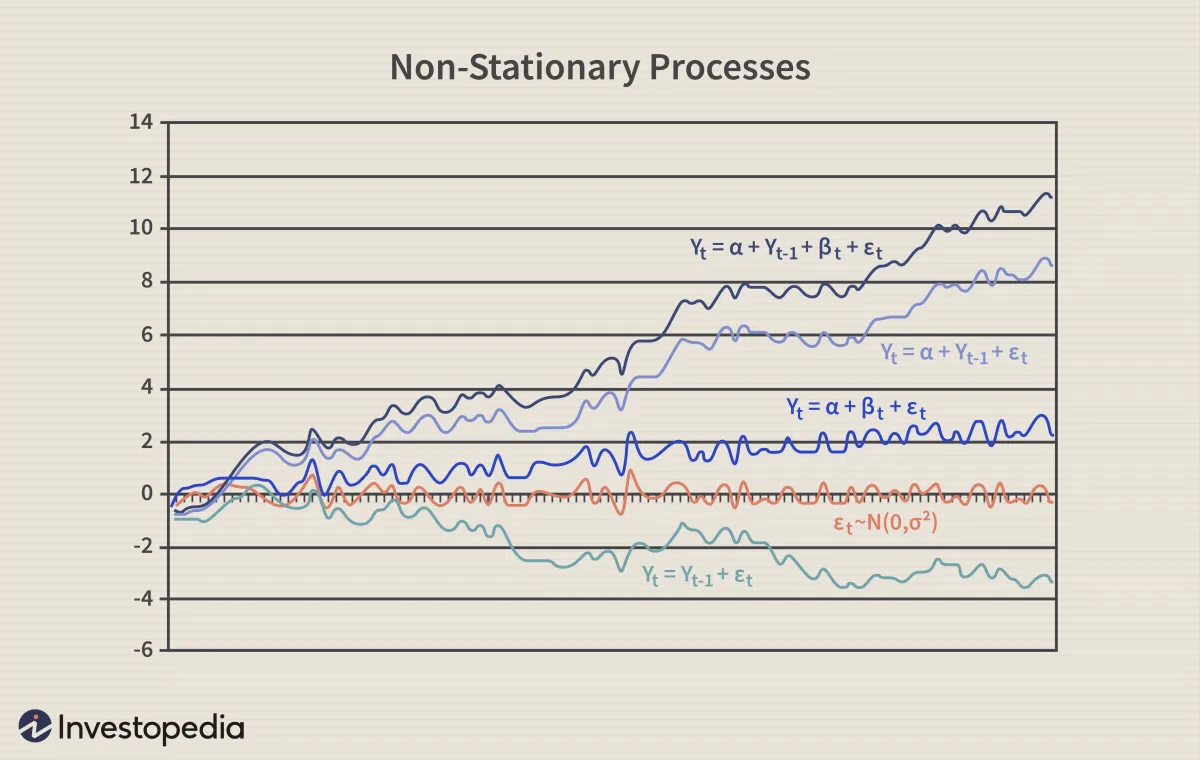
- 纯随机游走 (Y t = Y t-1 + ε t )随机游走预测时间“t”的值将等于上一周期值加上随机(非系统)分量,该分量是白噪声,这意味着 ε t是独立且相同分布的,均值为“0”,方差为“σ²”。随机游走也可以称为某种阶数的积分过程、具有单位根的过程或具有随机趋势的过程。它是一个非均值回归过程,可以正向或负向偏离均值。随机游走的另一个特征是方差随时间变化,并随着时间趋于无穷大;因此,随机游走无法预测。
- 带漂移的随机游走(Y t = α + Y t-1 + ε t )如果随机游走模型预测时间“t”的值将等于上一周期的值加上一个常数或漂移 (α) 和一个白噪声项 (ε t ),则该过程为带漂移的随机游走。它也不会恢复到长期平均值,并且具有随时间变化的方差。
- 确定性趋势 (Y t = α + βt + ε t )带有漂移的随机游走经常与确定性趋势混淆。两者都包括漂移和白噪声成分,但在随机游走的情况下,时间“t”的值回归于上一周期的值 (Y t-1 ),而在确定性趋势的情况下,它回归于时间趋势 (βt)。具有确定性趋势的非平稳过程的平均值围绕固定趋势增长,该趋势是恒定的并且与时间无关。
- 具有漂移和确定性趋势的随机游走 (Y t = α + Y t-1 + βt + ε t )另一个示例是将随机游走与漂移分量 (α) 和确定性趋势 (βt) 相结合的非平稳过程。它通过上一周期的值、漂移、趋势和随机分量来指定时间“t”的值。
趋势和差异平稳
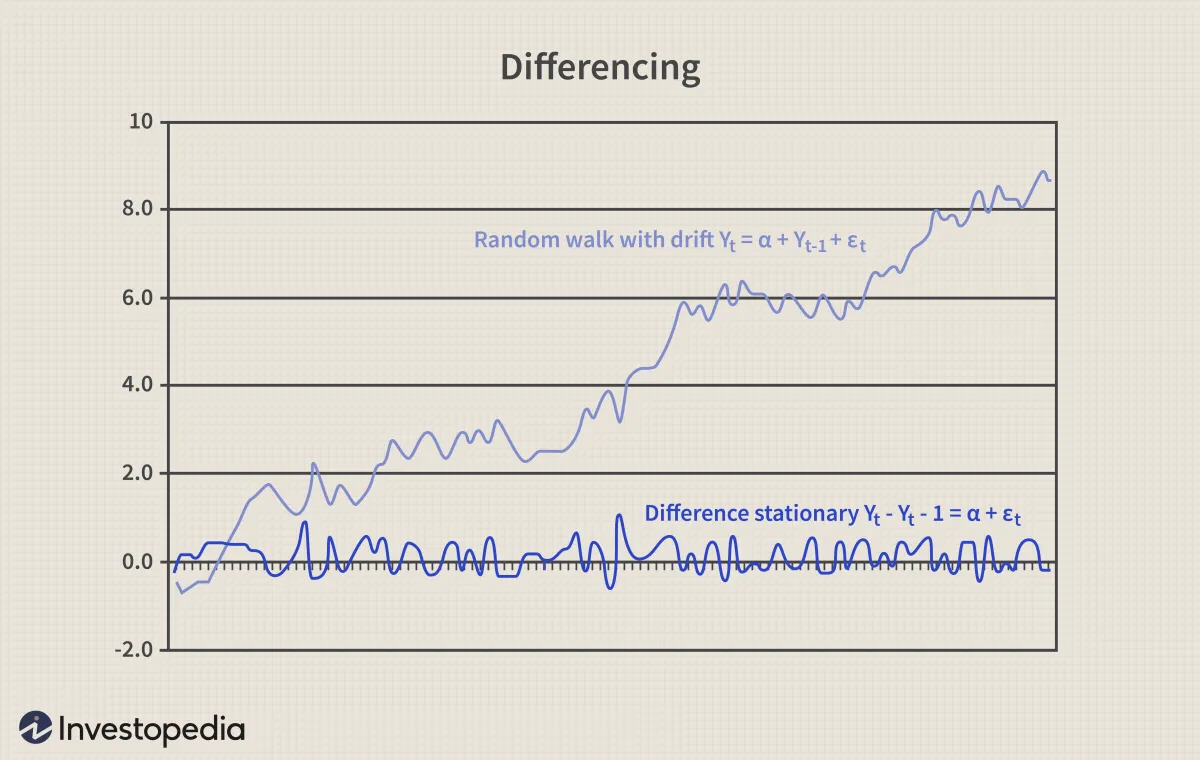
有或无漂移的随机游动都可以通过差分(从 Y t 中减去 Y t-1 ,取差分 Y t - Y t-1 )转换为平稳过程,对应于 Y t - Y t-1 = ε t或 Y t - Y t-1 = α + ε t ,然后该过程变为差分平稳。差分的缺点是每次取差分时,该过程都会丢失一个观测值。
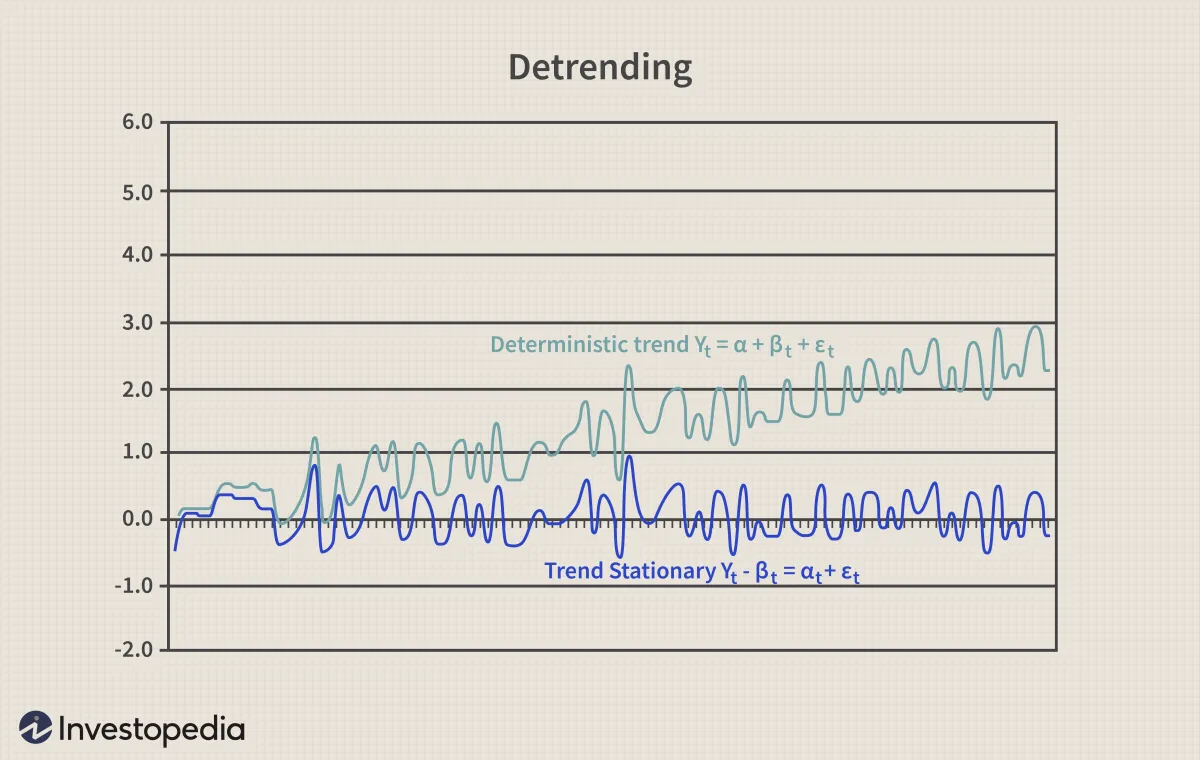
具有确定性趋势的非平稳过程在消除趋势(或去趋势)后变为平稳过程。例如,通过减去趋势 βt,Yt = α + βt + εt 可转换为平稳过程:Yt - βt = α + εt,如下图所示。当使用去趋势将非平稳过程转换为平稳过程时,不会丢失任何观察值。
对于具有漂移和确定性趋势的随机游走,去趋势可以消除确定性趋势和漂移,但方差将继续趋于无穷大。因此,还必须应用差分来消除随机趋势。
结论
在金融模型中使用非平稳时间序列数据会产生不可靠和虚假的结果,并导致理解和预测不佳。解决该问题的方法是转换时间序列数据,使其变为平稳的。如果非平稳过程是有或无漂移的随机游走,则通过差分将其转换为平稳过程。另一方面,如果所分析的时间序列数据表现出确定性趋势,则可以通过去趋势来避免虚假结果。
有时非平稳序列可能同时结合随机趋势和确定性趋势,为了避免获得误导性结果,应该同时应用差分和去趋势,因为差分将消除方差中的趋势,而去趋势将消除确定性趋势。