股票市場是一個相當複雜的系統,股票價格的變化受到經濟、有關行業、政治及投資者心理等多種因素的影響,各因素的影響程度、時間範圍和方式也不盡相同;且股市各因素間相互關係錯綜複雜,主次關係變化不定,數量關係難以提取及定量分析,因此我們需要尋找一種好的方法來避免或減弱這些因素的影響。
金融時序時間小波預測原理
現在常用的時間序列分析法主要是建立自迴歸模型(AR)、移動平均模型(MA),自迴歸一移動平均模型(ARMA)和齊次非平穩模型(ARIMA ),其中ARIMA模型是較成熟的模型,常被用來對股價(最高價、最低價、開盤價、收盤價)及綜合指數進行預測,通過選擇模型的參數和辨識模型的係數實現對時間序列的擬合,進而用擬合好的模型對未來進行預測。然而以上這些預測方法對於平穩時間序列均有較好的作用,對於非平穩時間序列則表現得不盡如人意。
小波函數具有自適應性和變焦特性,能有效地處理非平穩信號,可以將信號分解到不同的頻率通道上。由於分解後的信號在頻率成分上比原始信號單一,並且小波分解後對信號做平滑處理,然後重構分解信號,這樣非平穩時間序列經過處理後,成爲近似意義上的平穩時間序列,就能用一些傳統的預測方法對分解重構後的時間序列進行預測了。
採用小波進行金融時序數據預測的原理如下:使用Mallat算法對數據進行分解,對分解後的數據進行平滑處理,然後再進行重構,而重構之後的數據就成爲近似意義的平穩時間序列,這樣就得到了原始數據的近似信號,再應用AIC準則定階法判定AR[p]模型的階數。用最小二乘法估計參數αt的自相關係數p是否趨近於零,若趨近於零,模型適用,然後用AR[p]模型對重構後的數據進行預測,將預測結果與實際值進行比較,再與直接利用AR[p]模型對數據進行預測得到的預測誤差均方根值進行比較,得出結論如圖12-2所示。
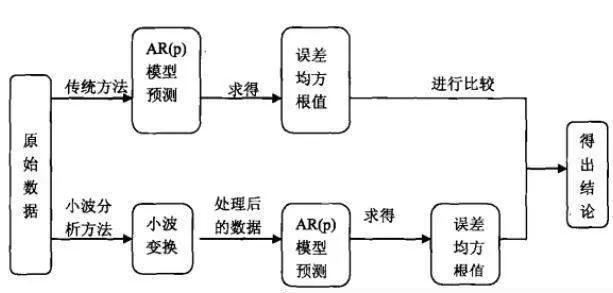
圖12-2 金融時序數據預側中小波方法和傳統方法的區別