筆
筆是纏論中由分型發展而來的一個重要概念,是纏論劃線分析方法的基礎概念。
筆的定義
兩相鄰頂分型和底分型頂底之間的連線叫做筆。
如圖1-33所示,AB是頂分型與底分型頂底之間的連線,AB叫做筆;BC是底分型和頂分型底頂之間的連線,BC也叫做筆。
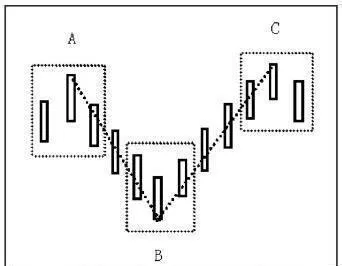
圖1-33 筆的定義
筆的最基本要求
頂分型和底分型之間至少有一根獨立K線。
如圖1-34所示,AB之間至少要有一根獨立的K線,這樣AB才能稱爲筆。
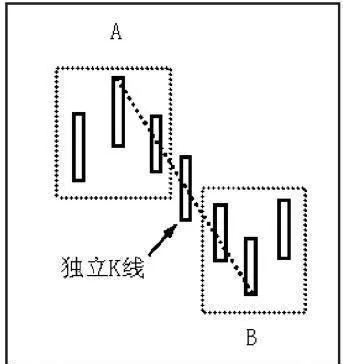
圖1-34
如圖1-35所示,CD之間至少要有一根獨立K線,這樣CD才能稱爲筆。
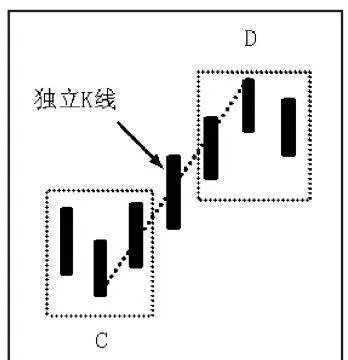
圖1-35
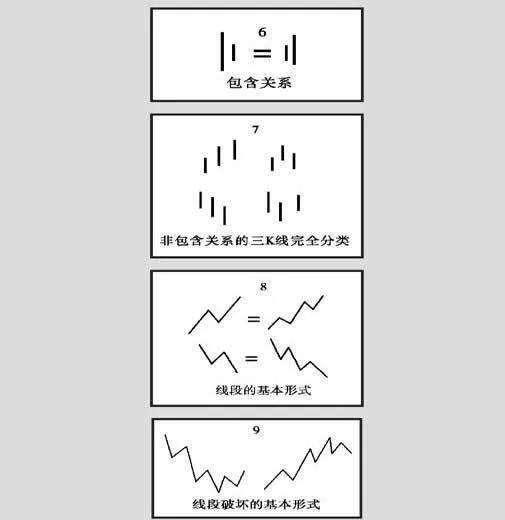
上升的一筆,由結合律分析,一定是底分型+上升K線+頂分型。下降的一筆,就是頂分型+下降K線+底分型。注意,這裏的上升、下降K線,不一定都是三根,可以是無數根,只要符合這個定義就可以。當然,簡單的也可以是一兩根,只要不違反結合律和定義。(教你炒股票62)
筆,必須是一頂一底,而且頂和底之間至少有一根K線不屬於頂分型與底分型。當然,還有一個最顯然的,就是在同一筆中,頂分型中最高那根K線的區間,至少要有一部分高於底分型中最低那根K線的區間。如果這條滿足不了,也就是頂都在底的範圍內,或頂比底還低,這顯然是不可接受的。(教你炒股票72)
在確定筆的過程中,必須要滿足上面的條件,這樣可以確定唯一的筆。這個劃分的唯一性很容易證明。假設有兩個都滿足劃分筆的條件,這兩個劃分要有所不同,必然是兩個劃分從第N-1筆以前都是相同的,從第N筆開始出現第一個不同,這個N可以等於1,這樣就是從一開始就不同。那麼第N-1筆結束的位置的分型,顯然對於兩個劃分的性質是一樣的,都是頂或底。對於是頂的情況,那麼第N筆,其底對於兩個劃分必然對應不同的底分型,否則這筆對兩個劃分就是相同的,這顯然矛盾。由於分型的劃分是唯一的,因此,兩種不同的劃分裏,在第N筆對應的底分型,在順序上必然有前後高低之分,而且在這兩個底之間不可能存在一個頂,否則這裏就不是一筆了。(教你炒股票72)
如果前面的底高於後面的底,那麼前面的劃分顯然是錯誤的。因爲按這種劃分,該筆是沒有完成的。一個底不經過一個頂後就有一個更低的底,這是最典型的筆沒完成的情況。(教你炒股票72)
如果前面的底不低於後面的底,那麼在下面一個頂分型出現前,如果有一個底分型低於前面的底,那麼這兩種劃分都是不正確的,所劃分的筆都是沒有完成的。如下面一個頂分型出現前,沒有一個底分型低於前面的底,那麼下面一個頂分型必然高於前面的底,因此前面的底和這個頂分型就是新的N+1筆,第N筆和第N+1筆就有了唯一的劃分,這與第N筆開始有不同劃分的要求相矛盾。(教你炒股票72)
從上面筆劃分的唯一性證明中,其實也知道劃分筆的步驟:一、確定所有符合標準的分型。二、如果前後兩個分型是同一性質的,對於頂,前面的低於後面的,只保留後面的,前面那個可以忽略掉。對於底,前面的高於後面的,只保留後面的,前面那個可以忽略掉。不滿足上面條件的,例如相等的,都可以先保留。三、經過步驟二的處理後,餘下的分型,如果相鄰的是頂和底,那麼就可以劃爲一筆。(教你炒股票72)
如果相鄰分型性質一樣,那麼必然有前頂不低於後頂,前底不高於後底。在連續的頂後,必須會出現新的底,把這連續的頂中最早出現一個和這新出現的底連在一起,就是新的一筆,中間的那些頂都可以忽略掉;在連續的底後,必然會出現新的頂,把連續的底中最先出現一個,和新出現的頂連在一起,就是新的一筆,而中間的那些底都可以忽略掉。顯然,經過上面三個步驟,所有的筆都可以唯一地劃分出來。(教你炒股票72)
如圖1-36所示,EF之間沒有獨立K線,EF就不能成爲筆。
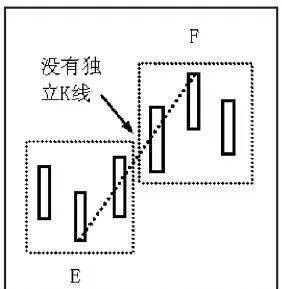
圖1-36
如圖1-37所示,GH之間沒有獨立K線,GH就不能成爲筆。
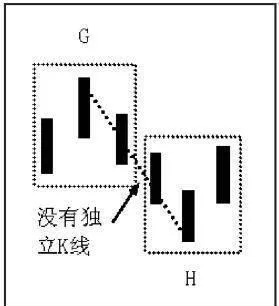
圖1-37
注意:筆中頂底之間所含獨立K線可以有一根,也可以有無數根。
如圖1-38所示,圖中箭頭所指處都爲筆。頂底之間所含獨立K線可以有多有少,但要求最少保持一根。
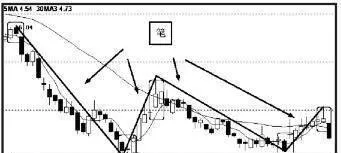
圖1-38