SVM算法是一種學習機制,是由Vapnik提出的旨在改善傳統神經網絡學習方法的理論弱點,最先從最優分類面問題提出了支持向量機網絡。SVM學習算法根據有限的樣本信息在模型的複雜性和學習能力之間尋求最佳折中,以期獲得最好的泛化能力。SVM在形式上類似於多層前向網絡,而且已被應用於模式識別、迴歸分析、數據挖掘等方面。
支持向量機這些特點是其他學習算法(如人工神經網絡)所不及的。對於分類問題,單層前向網絡可解決線性分類問題,多層前向網絡可解決非線性分類問題。但這些網絡僅僅能夠解決問題,並不能保證得到的分類器是最優的;而基於統計學習理論的支持向量機方法能夠從理論上實現對不同類別間的最優分類,通過尋找最壞的向量,即支持向量,達到最好的泛化能力。
SVM總的來說可以分爲線性SVM和非線性SVM兩類。線性SVM是以樣本間的歐氏距離大小爲依據來決定劃分的結構的。非線性的SVM中以卷積核函數代替內積後,相當於定義了一種廣義的趾離,以這種廣義距離作爲劃分依據。
模糊支持向量機有兩種理解:一種是針對多定義樣本或漏分樣本進行模糊後處理;另一種是在訓練過程中引入模糊因子作用。
SVM在量化投資中的應用主要是進行金融時序數列的預測。根據基於支持向量機的時間序列預測模型,先由訓練樣本對模型進行訓練和完備,然後將時間序列數據進行預測並輸出預測結果。
本章介紹的第一個案例是一種基於最小二乘法的支持向最機的複雜金融數據時間序列預測方法,大大提高了求解問題的速度和收斂精度。相比於神經網絡預測方法,該方法在大批量金融數據時間序列預測的訓練時間、訓練次數和預測誤差上都有了明顯提高,對複雜金融時間序列具有較好的預測效果。
第二個案例是利用SVM進行大盤拐點判斷,由於使用單一技術指標對股價反轉點進行預測存在較大的誤差,所以使用多個技術指標組合進行相互驗證就顯得特別必要。SVM由於採用了結構風險最小化原則,能夠較好地解決小樣本非線性和高維數問題,因此通過構造一個包含多個技術指標組合的反轉點判斷向最,並使用SVM對技術指標組合向量進行數據挖掘,可以得到更加準確的股價反轉點預測模型。
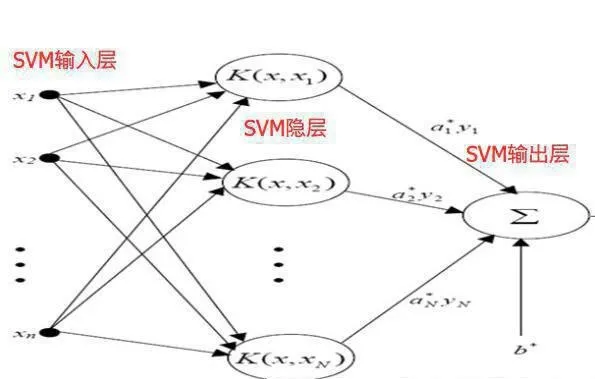
支持向量機基本概念
SVM算法是一種學習機制,是由Vapnik提出的旨在改善傳統神經網絡學習方法的理論弱點,最先從最優分類面問題提出了支持向量機網絡。
SVM學習算法根據有限的樣本信息在模型的複雜性和學習能力之間尋求最佳折中,以期獲得最好的泛化能力。SVM在形式上類似於多層前向網絡,而且己被應用於模式識別、迴歸分析、數據挖掘等方面。支持向量機方法能夠克服多層前向網絡的固有缺陷,它有以下幾個優點:
(1)它是針對有限樣本情況的。根據結構風險最小化原則,儘量提高學習機的泛化能力,即由有限的訓練樣本得到小的誤差,能夠保證對獨立的測試集仍保持小的誤差,其目標是得到現有信息下的最優解,而不僅僅是樣本數趨於無窮大時的最優值。
(2)算法最終將轉化成一個二次型尋優問題,從理論上說,得到的將是全局最優點。
(3)算法將實際問題通過非線性變換轉換到高維的特徵空間,在高維空間中構造線性判別函數來實現原空間中的非線性判別函數,這一特殊的性質能保證機器有較好的泛化能力,同時它巧妙地解決了維數災難問題,使得其算法複雜度與樣本維數無關。