K線的包含處理原則
K線走勢圖中,經常會看到一些有包含關係的K線。爲了準確識別K線走勢中的頂底分型,有必要對這些存在包含關係的K線進行包含處理。
所謂包含處理,就是將有包含關係的兩根K線合併成一根K線,即簡化處理。
K線包含處理分兩種情況:向上處理和向下處理。
①向上處理
存在包含關係的兩根K線合併時,當第一根K線的高點比其前一根具有非包含關係K線的高點高時,具有包含關係的兩根K線採取向上處理。
實際圖形裏,有些複雜的關係會出現,就是相鄰兩K線可以出現包含關係,也就是一K線的高低點全在另一K線的範圍裏,這種情況下,可以這樣處理,在向上時,把兩K線的最高點當高點,而兩K線低點中的較高者當成低點,這樣就把兩K線合併成一新的K線;反之,當向下時,把兩K線的最低點當低點,而兩K線高點中的較低者當成高點,這樣就把兩K線合併成一新的K線。經過這樣的處理,所有K線圖都可以處理成沒有包含關係的圖形。(教你炒股票62)
假設,第n根K線滿足第n根與第n+1根的包含關係,而第n根與第n-1根不是包含關係,那麼如果gn≥gn-1,那麼稱第n-1. n、n+1根K線是向上的;如果dn≤dn-1,那麼稱第n-1、n、n+1根K線是向下的。(教你炒股票65)
如圖1-4所示,圖左中B、C爲具有包含關係的兩相鄰K線,當B的高點比其前一根具有非包含關係K線A的高點高時,則B、C取向上處理。圖右中F、G爲具有包含關係的兩相鄰K線,當F的高點比其前一根具有非包含關係K線E的高點高時,則FG取向上處理。
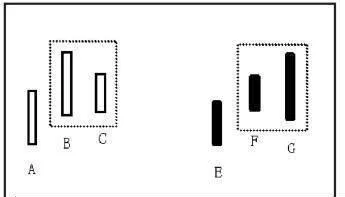
圖1-4
②向下處理
存在包含關係的兩根K線合併時,當第一根K線的高點比前一根具有非包含關係K線的高點低時,具有包含關係的兩根K線取向下處理。
如圖1-5所示,圖左中B、C爲具有包含關係的兩根K線,當B的高點比前一根非包含關係K線A的高點低時,則B、C取向下處理。圖右中F、G爲具有包含關係的兩根K線,當F的高點比前一根非包含關係K線E的高點低時,則F、G取向下處理。
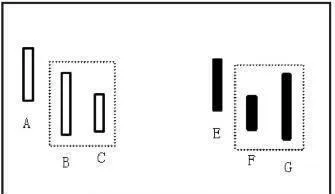
圖1-5
圖1-6爲向上處理及向下處理實圖。圖中B比A高,取向上處理;圖中D比C低,取向下處理。
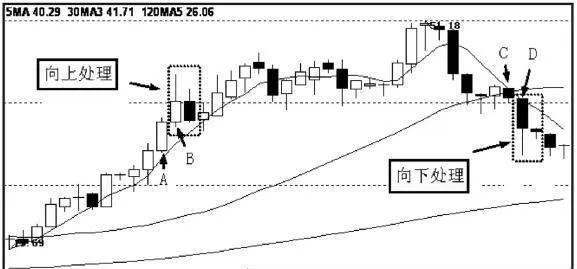
圖1-6
①向上處理的原則
K線包含向上處理時,取兩根K線中的最高點爲高點,較低點爲低點,合併成一根新K線。如圖1-7所示,B、C向上處理,取兩根K線中的最高點爲高點,較低點爲低點,合併成新K線D。
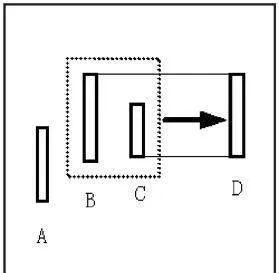
圖1-7
如圖1-8所示,F、G向上處理,取兩根K線中的最高點爲高點,較低點爲低點,合併成新K線H。
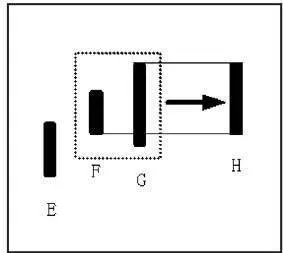
圖1-8
②向下處理的原則
K線包含向下處理,取兩根K線中最低點爲低點,較高點爲高點,合併成一根新K線。如圖1-9所示,B、C向下處理,取兩根K線中最低點爲低點,較高點爲高點,合併成新K線D。
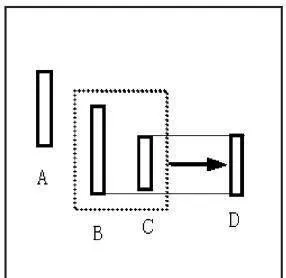
圖1-9
如圖1-10所示,FG向下處理,取兩根K線中最低點爲低點,較高點爲高點,合併成新K線H。
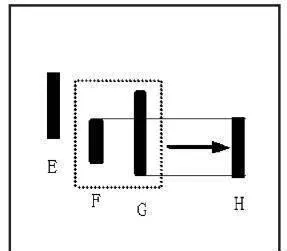
圖1-10