纏論第67課:線段劃分的標準
筆的劃分標準前面已經嚴格給出,下一個關鍵問題,就是如何劃分線段。下面給出類似筆劃分但有重大區別的劃分標準。用S代表向上的筆,X代表向下的筆。那麼所有的線段無非分爲兩種:(1)從向上筆開始的線段。(2)從向下筆開始的線段。簡單起見,下面以向上筆開始的線段爲例子說明線段劃分的標準。
以向上筆開始的線段,可以用筆的序列表示:S1X1S2X2S3X3…SnXn。容易證明,任何Si與Si+1之間,一定有重合區間。而考察序列X1X2…Xn,該序列中,Xi與Xi+1之間並不一定有重合區間,因此這一序列更能代表線段的性質。
定義:序列X1X2…Xn稱爲以向上筆開始的線段的特徵序列;序列S1S2…Sn稱爲以向下筆開始的線段的特徵序列。特徵序列兩相鄰元素間沒有重合區間,稱爲該序列的一個缺口。
關於特徵序列,把每一元素看成是一根K線,那麼如同一般K線圖中找分型的方法,也存在所謂的包含關係,也可以對此進行非包含處理。經過非包含處理的特徵序列,稱爲標準特徵序列。以後沒有特別說明,特徵序列都是指標準特徵序列。

上圖所示爲特徵序列、缺口等相關概念分析圖
參照一般K線圖關於頂分型與底分型的定義,可以確定特徵序列的頂和底。注意,以向上筆開始的線段的特徵序列,只考察頂分型;以向下筆開始的線段,只考察底分型。
在標準特徵序列裏,構成分型的三個相鄰元素,只有以下兩種可能。
1.特徵序列的頂分型中,第一和第二元素間不存在特徵序列的缺口,那麼該線段在該頂分型的高點處結束,該高點是該線段的終點;特徵序列的底分型中,第一和第二元素間不存在特徵序列的缺口,那麼該線段在該底分型的低點處結束,該低點是該線段的終點。
2.特徵序列的頂分型中,第一和第二元素間存在特徵序列的缺口,如果從該分型最高點開始的向下一筆開始的序列的特徵序列出現底分型,那麼該線段在該頂分型的高點處結束,該高點是該線段的終點;特徵序列的底分型中,第一和第二元素間存在特徵序列的缺口,如果從該分型最低點開始的向上一筆開始的序列的特徵序列出現頂分型,那麼該線段在該底分型的低點處結束,該低點是該線段的終點。
在第二種情況下,後一特徵序列不一定封閉前一特徵序列相應的缺口,而且第二個序列中的分型不分第一和第二種情況,只要有分型就可以。
上面兩種情況,就給出了所有線段劃分的標準。顯然,出現特徵序列的分型,是線段結束的前提條件。本課就是把前面“線段破壞的充要條件就是被另一個線段破壞”精確化了。因此以後關於線段的劃分,都以此精確的定義爲基礎。
這個定義有點複雜,首先請先搞清楚特徵序列,然後搞清楚標準特徵序列,然後是標準特徵序列的頂分型與底分型。分型又以分型的第一元素和第二元素間是否有缺口分爲兩種情況。一定要把這個邏輯關係搞清楚,否則一定暈倒。
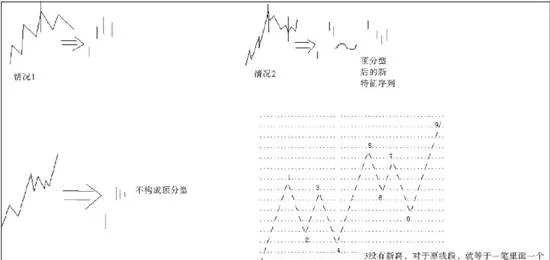
上圖爲兩種情況線段劃分示意圖
顯然,按照這個劃分,一切同一級別圖上的走勢,都可以唯一地劃分爲線段的連接,正如一切同一級別圖上的走勢,都可以唯一地劃分爲筆的連接一樣。有了這兩個基礎,那麼整個中樞與走勢類型的遞歸體系就可以建立起來。這是基礎的基礎,請務必搞清楚,否則肯定學不好。
最後,儘量畫點圖,讓各位分清楚上面的一些概念。但最好把定義看清楚,這纔是真正理解,圖只是一個輔助。前兩個圖形中標出了線段的劃分。
纏論點睛
1.所謂特徵序列,是指線段中所有與線段方向相反的筆構成的集合;所謂標準特徵序列,是指經過非包含處理的特徵序列。特徵序列非包含處理的方法和K線的非包含處理方法是一樣的。
2.某級別上漲之後的回調不能破前高,或者下跌之後的回抽不能破前低,就會形成特徵序列的缺口。一般這種走勢都是極爲強烈的。
3.標準特徵序列分型中,同樣會出現頂分型連着頂分型或者底分型連着底分型的情況,對於這種情況,其中某一個只能算作中繼特徵序列分型。處理方法與K線中的處理方法一致。
投資微言
大多數人都是容易買對,永遠賣不對,結果就是坐電梯。這種情況說白了,就是貪婪所致。寧願賣早,不要賣晚。賣晚,不僅坐電梯,還錯過了好的機會。