從本章開始，會應用和上一章相同的名詞，比如盤整、趨勢等，但都與上一章毫無關係。因爲文字表達的侷限性，對不同的概念只能用相同的名詞表述，但這並不意味着二者是一回事。均線構成的操作系統是單獨的章節，與本章的中樞系統有本質上的不同，請各位注意。

再次重申，關於盤整、趨勢、走勢類型，在均線構成的操作系統與由中樞構成的操作系統中，含義是不同的，千萬不要混淆。在均線系統中，盤整、上漲、下跌都是圖形特徵，在圖中是盤整的就叫盤整，看起來是上漲的就是上漲，圖中呈現下跌的就是下跌，上漲和下跌都是走勢形態的分類。在本章開始的中樞系統中，盤整與下跌是有嚴格定義的，有些在圖中看起來是上漲的走勢，根據本章的內容有可能會被定義爲盤整。這是兩種不同的概念表述，仔細區分應該不難辨別。

在纏論原文中，用數學公式的形式來定義走勢中樞的區間當然是最精確的，但很多數學不太好的要理解這種抽象的公式比較困難，所以筆者儘量說得通俗一點。

第一，走勢中樞是有級別的，按慣用的級別系統，分別有1分鐘以下、1分鐘、5分鐘、30分鐘、日線、周線、月線級別中樞。

第二，某級別的走勢中樞，至少由次級別連續三段完成的走勢類型重疊而成，中樞區間就是三段完成的走勢類型的價格重疊區間。

第三，根據走勢必完美，任何級別的任何走勢類型，都必然由次級別三段完成的走勢類型連接而成。

第四，在任意走勢類型中，走勢類型的級別由走勢中樞的級別確定。從第二和第三可以得出：走勢必完美基本等同於任意級別的任意走勢類型一定能形成該級別中樞。

第一點中的級別問題應該不難理解，難的是如何劃分級別。要解決這個問題，就需要理解第二點中的“三段”“連續的”“完成的”“次級別走勢類型”“價格重疊區間”“中樞區間”五個關鍵詞。

三段：上一章中闡述過，就是次級別三段走勢的連接，這裏排除上漲加上漲的連接方式，因爲同向走勢的連接還是一個走勢類型。

連續的：這更好理解，第一段結束跟着第二段，第二段結束跟着第三段，其間不能斷開，隔一個計算。

完成的次級別走勢類型：任意級別的走勢類型都必須在次級別上形成三段完成走勢類型的連接才能完成，這是走勢必完美。這裏從純理論的角度來看，存在循環定義的問題。簡單的處理辦法，就是前面一章中說的用均線是否黏合、交叉、纏繞來判斷完成的走勢類型。顯然，一段下跌走勢，長短均線一直保持向下沒有什麼波動的，一定是次級別或者次級別以下級別走勢類型，只有出現波動並形成該級別中樞，才能稱爲本級別走勢精細地分析某級別中樞，需要次級別三段完成的走勢類型，這次級別的三段走勢類型的任意一段要完成，又要下一級次級別三段走勢類型。這樣遞歸下來，一定會遇到最低級別走勢類型如何定義的問題，這個難題可以通過對操作級別的定義來解決。

當確定操作級別以後，比如在操作系統中按30分鐘級別操作，那麼在30分鐘操作級別的視角下，就可以規定次級別也就是5分鐘級別走勢爲最低級別。一般的軟件都可以看到1分鐘K線圖，但在30分鐘級別的操作系統中是不看的，如果按5分鐘來定義操作級別，就需要把1分鐘作爲最低級別處理。在30分鐘操作級別的前提下，也就相當於默認軟件最低只能顯示5分鐘K線圖。在5分鐘K線走勢圖中，將連續三根K線橫盤的區域作爲次級別走勢中樞處理，其實也就是把每一根5分鐘K線作爲5分鐘的次級別的次級別處理。

圖2-1最小級別中樞與重疊形成高級別中樞示意圖

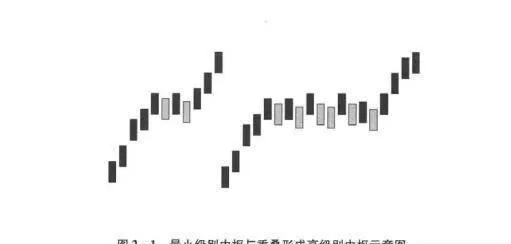
圖2-1爲了簡單示意，忽略了上下影線，但原理都是相同的，對結果並沒有影響。左邊從第六根K線開始盤整，連續三根K線構成次級別中樞後，突破中樞上漲。右邊是九根K線重疊的情況，這種情況因爲每三根K線構成次級別中樞，三個次級別中樞就構成高一級別的中樞，所以是本級別的中樞，走勢爲本級別的走勢類型。

對於左邊的圖，如果你已經對上一章中，由均線構成的操作系統熟悉的話，就應該知道，這是次級別以下級別上漲+盤整+上漲的走勢類型連接。應用中，對於盤整區域左邊的上漲、盤整區域、盤整區域右邊的上漲，一律定義爲次次級別走勢類型。這樣，由三段次次級別走勢類型連接而成的次級別走勢類型就形成了，根據中樞的定義，中間重疊部分爲次級別中樞。

次級別走勢類型定義後，就可以在圖中找到任意級別走勢類型的中樞區域。而因爲走勢必完美，任何級別的任何走勢類型一定能形成至少一個該級別中樞。至此，就可以對盤整與趨勢進行精確定義，其中趨勢分爲上漲與下跌。

盤整：只有一箇中樞的走勢類型，稱爲該中樞級別的盤整走勢類型。趨勢：依次順向形成兩個互不重疊的同級別中樞的走勢類型，稱爲該中樞級別的趨勢走勢類型，兩個中樞依次向下就是下跌趨勢，反之就是上漲趨勢。

相關文章