利率变化影响整体经济、股票市场、债券市场和其他金融市场,并能影响宏观经济因素。利率的变化也会影响期权估值,这是一项涉及多种因素的复杂任务,包括标的资产的价格、行权或执行价格、到期时间、无风险回报率(利率)、波动性和股息收益率。除执行价格外,所有其他因素都是未知变量,在期权到期之前都可能发生变化。
定价选项的利率是多少?
了解定价选项中使用的正确到期利率非常重要。大多数期权估值模型(例如布莱克-斯科尔斯)都使用年化利率。
如果生息账户每月支付 1%,您将获得 1%*12 个月 = 12% 的年利息。正确的?
不!不同时间段内的利率转换的工作方式与简单的时间段的向上(或向下)缩放乘法(或除法)不同。假设您的月利率为每月 1%。如何将其转换为年利率?在这种情况下,时间倍数 = 12 个月/1 个月 = 12:
- 将月利率除以 100(得到 0.01)
- 加 1(得到 1.01)
- 将其计算为时间倍数次方(即 1.01^12 = 1.1268)
- 从中减去 1(得到 0.1268)
- 乘以100,即为年利率(12.68%)
这是任何涉及利率的估值模型中使用的年化利率。对于像布莱克-斯科尔斯这样的标准期权定价模型,使用无风险的一年期国债利率。
值得注意的是,利率变动并不频繁且幅度较小(通常增量为 0.25%,或仅 25 个基点)。决定期权价格的其他因素(如标的资产价格、到期时间、波动性和股息收益率)变化更频繁、幅度更大,与利率变化相比,这些因素对期权价格的影响相对更大。
要点
- 利率的变化直接影响期权定价,其计算由众多复杂因素组成。
- 对于Black-Scholes等标准期权定价模型,使用无风险年化国债利率。
- 当利率上升时,看涨期权受益,而看跌期权价格受到负面影响。
利率如何影响看涨期权和看跌期权价格
为了理解利率变化影响背后的理论,股票购买和同等期权购买之间的比较分析将是有用的。我们假设专业交易者用带息借钱进行多头头寸交易,并通过空头头寸获得生息资金。
看涨期权的利息优势
以 100 美元的价格购买 100 股股票将需要 10,000 美元,假设交易者借钱进行交易,则需要支付这笔资金的利息。以 12 美元的价格购买 100 份合约的看涨期权仅需花费 1,200 美元。然而,利润潜力将与多头股票头寸保持相同。
实际上,8,800 美元的差额将节省这笔贷款金额的支出利息。或者,节省下来的 8,800 美元资本可以保留在计息账户中,并产生利息收入——5% 的利息一年后将产生 440 美元。
因此,利率上升将导致贷款金额的支出利息节省或储蓄账户利息收入的增加。两者都对该看涨期权头寸+储蓄有利。实际上,看涨期权的价格上涨反映了利率上升带来的好处。
看跌期权的利息劣势
从理论上讲,为了从价格下跌中受益而做空股票将为卖空者带来现金。购买看跌期权也能从价格下跌中获得类似的好处,但需要支付看跌期权溢价。这种情况有两种不同的情况:通过做空股票收到的现金可以为交易者赚取利息,而购买看跌期权所花费的现金则是应付利息(假设交易者借钱购买看跌期权)。
随着利率上升,做空股票比买入看跌期权更有利可图,因为前者产生收入,而后者则相反。因此,看跌期权价格受到利率上升的负面影响。
罗希腊语
Rho是标准希腊语,用于衡量利率变化对期权价格的影响。它表示利率每变化 1%,期权价格将变化的量。假设看涨期权当前定价为 5 美元,rho 值为 0.25。如果利率增加 1%,则看涨期权价格将增加 0.25 美元(至 5.25 美元)或其 rho 值。同样,看跌期权价格将减少其 rho 值。
由于利率变化不会频繁发生,并且通常以 0.25% 为增量,因此 rho 不被视为主要希腊因子,因为与其他因子(或希腊因子,如 delta、gamma)相比,它不会对期权价格产生重大影响。 、织女星或西塔)。
利率变化如何影响看涨期权和看跌期权价格?
以标的交易价格为 100 美元的欧式价内(ITM)看涨期权为例,行权价为 100 美元,到期日为一年,波动率为 25%,利率为 5%,使用 Black-Scholes 模型的看涨期权价格为 12.3092 美元,看涨期权 rho 值为 0.5035。具有类似参数的看跌期权价格为 7.4828 美元,看跌期权 rho 值为 -0.4482(情况 1)。
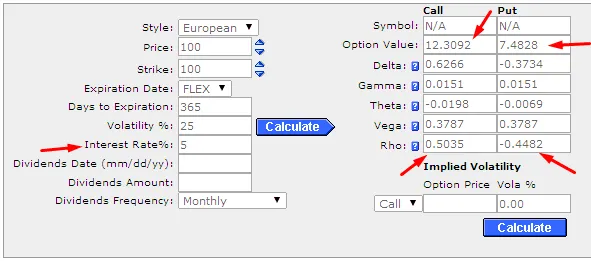
资料来源:芝加哥期权交易所(CBOE)
现在,我们将利率从 5% 提高到 6%,其他参数保持不变。
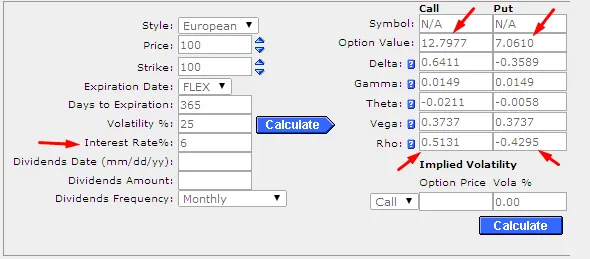
看涨期权价格已上涨至 12.7977 美元(变化为 0.4885 美元),看跌期权价格已下跌至 7.0610 美元(变化为 -0.4218 美元)。看涨期权价格和看跌期权价格的变化量与之前计算的看涨期权 rho (0.5035) 和看跌期权 rho (-0.4482) 值几乎相同。 (分数差异是由于 BS 模型计算方法造成的,可以忽略不计。)
事实上,利率通常仅以 0.25% 的增量变化。举一个现实的例子,我们将利率从 5% 改为 5.25%。其他数字与情况1相同。
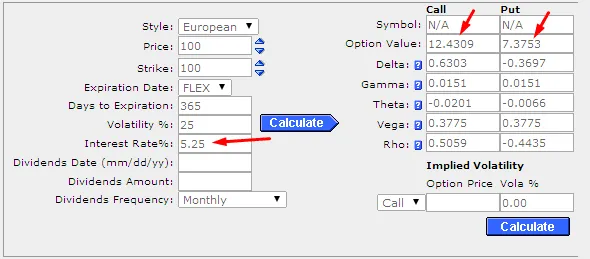
看涨期权价格增至 12.4309 美元,看跌期权价格降低至 7.3753 美元(看涨期权价格小幅变化 0.1217 美元,看跌期权价格小幅变化 - 0.1075 美元)。
可以看出,利率变化 0.25% 后,看涨期权和看跌期权价格的变化可以忽略不计。
利率可能会在一年内变化四次(4 * 0.25% = 1% 增加),即直到到期时间。尽管如此,此类利率变化的影响可能可以忽略不计(对于 12 美元的 ITM 看涨期权价格和 7 美元的 ITM 看跌期权价格,仅约 0.5 美元)。在一年中,其他因素的变化幅度可能要大得多,并且可能会对期权价格产生重大影响。
对虚值 (OTM) 和 ITM 期权进行类似的计算会产生类似的结果,但在利率变化后,期权价格仅观察到微小的变化。
套利机会
是否有可能从预期利率变化的套利中受益?通常,市场被认为是有效的,并且期权合约的价格已经被假定包含任何此类预期变化。
此外,利率的变化通常会对股票价格产生反向影响,这对期权价格的影响要大得多。总体而言,由于利率变化导致期权价格变化较小,套利收益难以利用。
综述
期权定价是一个复杂的过程,并且不断发展,尽管布莱克-斯科尔斯等流行模型已经使用了几十年。影响期权估值的因素有多种,这可能导致期权价格在短期内出现很大的变化。看涨期权和看跌期权的溢价随着利率的变化而受到相反的影响。然而,对期权价格的影响很小;期权定价对其他输入参数的变化更加敏感,例如基础价格、波动性、到期时间和股息收益率。