什么是波动率微笑?
波动率微笑是一种常见的图形形状,它通过绘制一组具有相同标的资产和到期日的期权的执行价格和隐含波动率而得出。波动率微笑之所以如此命名,是因为它看起来像一张微笑的嘴。当期权的标的资产相对于平价(ATM) 而言进一步处于虚值(OTM) 或实值(ITM) 时,隐含波动率就会上升。波动率微笑并不适用于所有期权。
重点
- 当具有相同到期日和相同标的资产,但执行价格不同的期权的隐含波动率图表被绘制出来时,该图表往往会呈现出微笑状。
- 微笑表明价内 (ITM) 或价外 (OTM) 最远的期权具有最高的隐含波动率。
- 隐含波动率最低的期权的执行价格为平价(ATM)或接近平价。
- 并非所有期权都会出现隐含波动率微笑。短期股票期权和货币相关期权更有可能出现波动率微笑。
- 单一期权的隐含波动率也可能随着其价值或价外波动而遵循波动率微笑。
- 虽然隐含波动率是期权定价的一个因素,但它并不是唯一因素。交易者必须了解哪些其他因素正在推动期权的价格和波动率。
波动率微笑告诉您什么?
波动率微笑是由隐含波动率随着标的资产的 ITM 或 OTM 变动而变化而产生的。期权的 ITM 或 OTM 变动越大,其隐含波动率就越大。ATM 期权的隐含波动率往往最低。
布莱克-斯科尔斯模型是用于为期权和其他衍生品定价的主要公式之一,但它并没有预测到波动率微笑。布莱克-斯科尔斯模型预测,隐含波动率曲线在与不同的执行价格相对时是平坦的。根据该模型,可以预期,对于在同一天到期且具有相同标的资产的所有期权,无论执行价格如何,隐含波动率都是相同的。然而,在现实世界中,情况并非如此。
1987 年股市崩盘后,期权定价开始出现波动率微笑。此前,美国市场并不存在这种现象,这表明市场结构更符合 Black-Scholes 模型的预测。1987 年之后,交易员意识到极端事件可能发生,市场存在显著偏差。期权定价需要考虑到极端事件发生的可能性。因此,在现实世界中,随着期权的 ITM 或 OTM 变动,隐含波动率会增加或减少。
此外,波动率微笑的存在表明,ITM 和 OTM 期权的需求往往比 ATM 期权更大。需求推动价格,从而影响隐含波动率。这可能部分是由于上述原因。极端事件可能会发生,导致期权价格发生重大变化。隐含波动率会考虑到发生大幅变化的可能性。
如何使用波动率微笑的示例
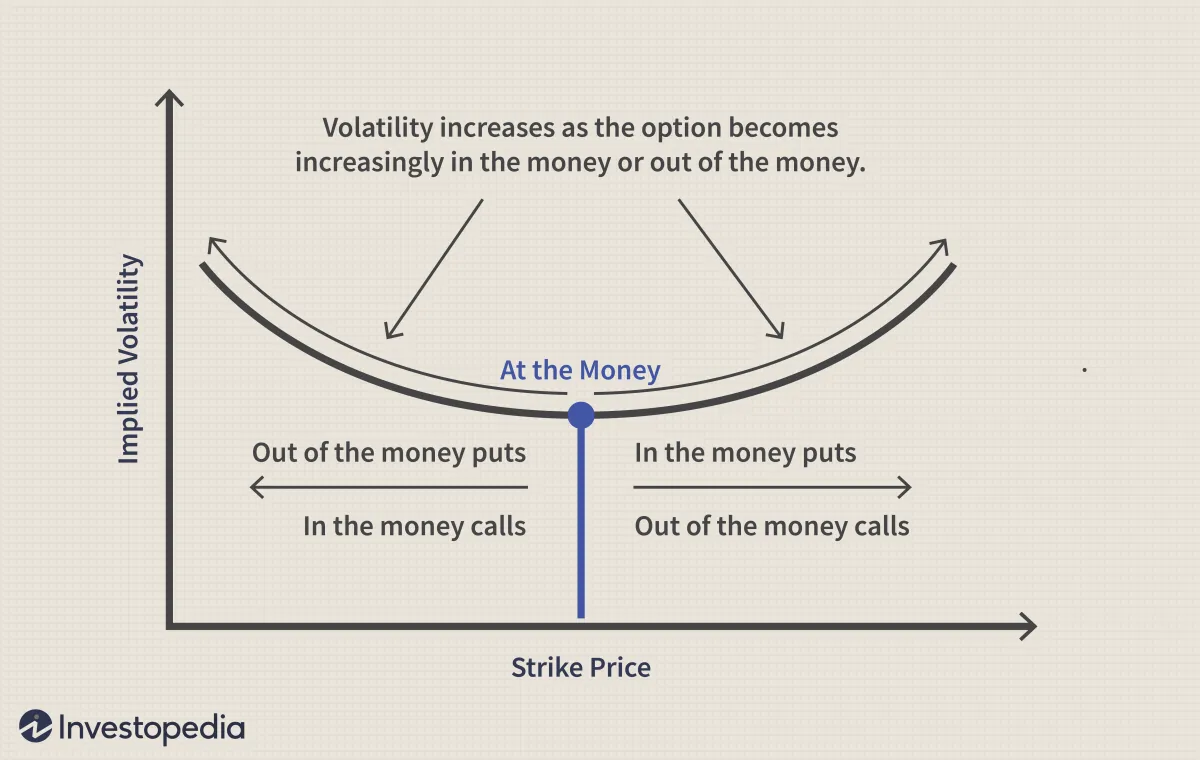
当比较具有相同标的资产和相同到期日但不同执行价格的各种期权时,可以看到波动率微笑。如果绘制每个不同执行价格的隐含波动率,则可能出现 U 形。U 形并不总是像上图所示的那样完美。
要粗略估计期权是否具有 U 形,请调出列出各种执行价格的隐含波动率的期权链。如果期权具有 U 形,则 ITM 和 OTM 相等的期权应具有大致相同的隐含波动率。ITM 或 OTM 越远,隐含波动率就越大,ATM 期权附近的隐含波动率最低。如果不是这种情况,则该期权不符合波动率微笑。
单一期权的隐含波动率也可以相对于标的资产的价格随时间变化绘制。随着价格在价内或价外波动,隐含波动率可能呈现某种 U 形。
如果寻求具有较低隐含波动率的期权,这可能很有用。在这种情况下,选择一个接近价内期权。如果寻求更大的隐含波动率,请选择更接近价内或价外的期权。但请记住,随着标的资产接近或远离执行价格,这将影响隐含波动率。因此,维持具有特定隐含波动率的期权组合将需要不断重新调整。
并非所有期权都符合波动率微笑。在使用波动率微笑辅助做出交易决策之前,请检查以确保期权的隐含波动率确实遵循微笑模型。
波动率微笑与波动率倾斜/假笑之间的区别
虽然短期股票期权和外汇期权更倾向于与波动率微笑保持一致,但指数期权和长期股票期权往往更倾向于与波动率倾斜保持一致。倾斜/微笑表明,ITM 或 OTM 期权的隐含波动率可能更高。
使用波动率微笑的局限性
首先,确定所交易的期权是否真正符合波动率微笑非常重要。波动率微笑是期权可能符合的一种模型,但隐含波动率可能更符合反向或正向倾斜/微笑。
此外,由于其他市场因素,例如供求关系,波动率微笑(如果适用)可能不是干净的 U 形(或微笑)。它可能具有基本的 U 形,但可能会波动,某些期权的隐含波动率可能高于或低于基于模型的预期。
波动率微笑凸显了交易者在希望获得更大或更小的隐含波动率时应该关注的地方,然而,在做出期权交易决策时还需要考虑许多其他因素。