走勢中樞定義概述
某級別走勢類型中被至少前三個連續次級別的走勢類型所重疊的部分稱爲走勢中樞。走勢中樞其實就是買賣雙方反覆較量的過程。走勢中樞越簡單,證明其中一方的力量越強大。
走勢中樞的複雜程度是考察市場最終動向的一個很重要的依據。一個超複雜的走勢中樞過後,就算一方贏了,其後的走勢也是經常反覆不斷的。
在同一趨勢中,相鄰兩走勢中樞的複雜程度與形態經常有所區別,爲什麼?很多人操作時都有提前量,而提前量經常就是找最近的樣本去模仿,這樣等於在買賣的合力中,都增加了一個提前的變量這樣一個分力,這樣就造成整個結構的變化。這是一個很重要的原理,其本質上是由人的貪嗔癡疑慢造成的。
如圖7-1所示。
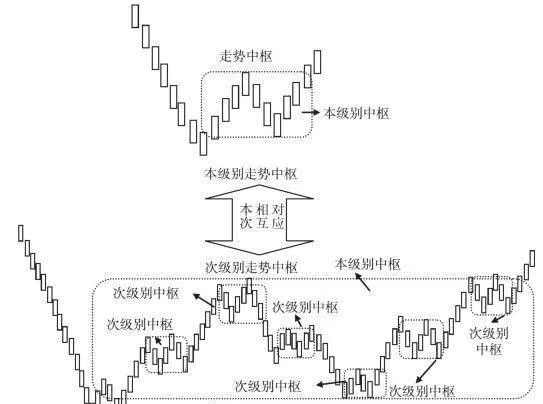
圖7-1 本級別的由次級別走勢類型形成的走勢中樞
走勢中樞定義的關鍵,在於定義的遞歸性。
遞歸定義由兩部分組成,一、f1(a0)=a1。二、f2(an)=an+1。第一條,其實可以隨意設置,都不會改變走勢中樞定義的遞歸性。
f1,f2可以是完全不同的兩個函數。可以用分型、線段這樣的函數關係構造最低級別的走勢中樞、走勢類型,也就是一中的a1。可以用另外的函數關係,也就f2去定義更高級別的走勢中樞或者走勢類型。
一個研究對象的確立,特別是一個數學和幾何對象的確立,首先要證明其存在。例如走勢中樞或走勢類型這兩個對象,如果不能證明其一定存在,而且是按級別存在的,那麼就沒有談論意義了。
前面關於走勢中樞的遞歸定義,就是解決這個問題的,是解決存在性問題。也就是說,走勢中樞是可以以遞歸的方式定義出來的,而該定義是具有可操作性的。該定義實際上是如何找出走勢中樞的一種方法,按照這種方法,肯定能找出定義中的走勢中樞。因此對於走勢中樞和走勢類型,也就有了關於不同不同級別圖形的研究。否則都從最原始的分筆成交去逐步定義和尋找,非常麻煩,也沒什麼操作性了。