纏論第65課:再說分型,筆和線段
本ID反覆強調,本ID理論的關鍵是一套幾何化的思維,因此你需要從最基本的定義出發。這一點在實際操作的辨認中更爲重要。所有複雜的情況,其實從最基本的定義出發,都沒有任何困難可言。
例如對於分型,其中最大的麻煩,就是所謂的前後K線之間的包含關係。其次,有點簡單的幾何思維,根據定義,任何人都可以馬上得出以下一些推論。
1.用[di,gi]代表第i根K線的最低點和最高點構成的區間。當向上時,順次n個具有包含關係的K線組,等價於[maxdi,maxgi]的區間對應的K線。也就是說,這n個K線,和最低最高區間爲[maxdi,maxgi]的K線是一回事情。向下時,順次n個包含關係的K線組,等價於[mindi,mingi]的區間對應的K線。
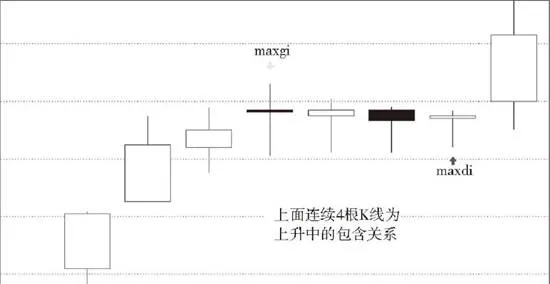
上圖所示爲上升中的包含關係示意圖
2.結合律是本ID理論中最基礎的定律,在K線的包含關係處理中,當然也需要遵守。但包含關係不符合傳遞律,也就是說,第1根、第2根K線是包含關係,第2根、第3根也是包含關係,但並不意味着第1根、第3根就有包含關係。因此在K線包含關係的分析中,還要遵守順序原則,就是先用第1根、第2根K線的包含關係確認新的K線,然後用新的K線去和第3根比較。如果有包含關係,繼續用包含關係的合併法則結合成新的K線;如果沒有,就按正常K線處理。
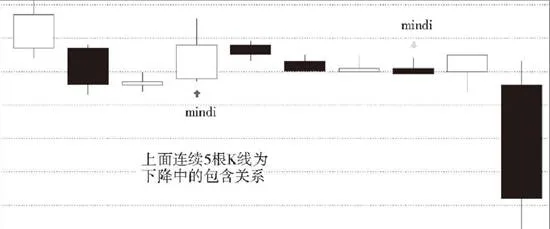
上圖所示爲下降中的包含關係示意圖
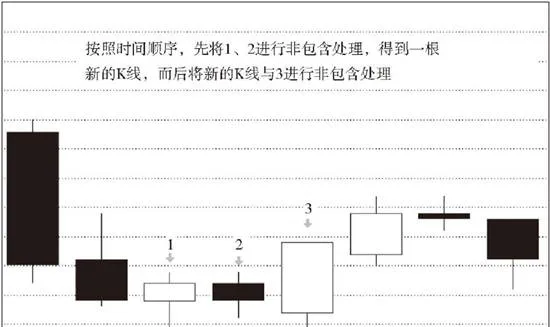
上圖所示爲順序處理包含關係示意圖
3.有人可能還要問,什麼是向上?什麼是向下?其實這根本沒什麼可說的,任何看過圖的人都知道什麼是向上,什麼是向下。當然,本ID的理論是嚴格的幾何理論,對向上向下,也可以嚴格地定義。
假設第n根K線滿足第n根與第n+1根的包含關係,而第n根與第n-1根不是包含關係,那麼如果gn≥gn-1,那麼稱第n-l、n、n+1根K線是向上的;如果dn≤dn-1,那麼稱第n-1. n、n+1根K線是向下的。
有人可能又要問,如果gn<gn-1且dn>dn-1,這算什麼?那就是一種包含關係,就違反了前面第n根與第n-1根不是包含關係的假設。同樣道理,gn≥gn-1與dn≤dn-1不可能同時成立。
上面包含關係的定義已經十分清楚,都是一些最精確的幾何定義。只要按照定義來做,沒有任何圖是不可以精確無誤地、按統一的標準去找出所有的分型來的。
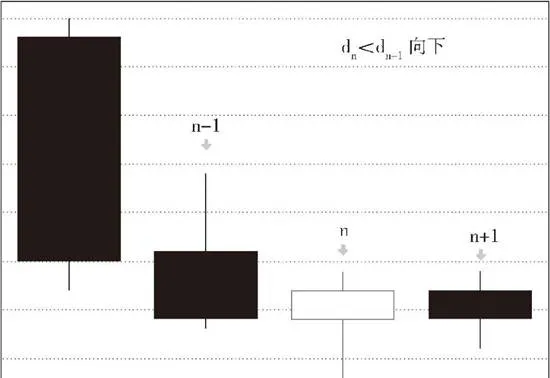
上圖是第n-n、n+1根K線向下關係示意圖
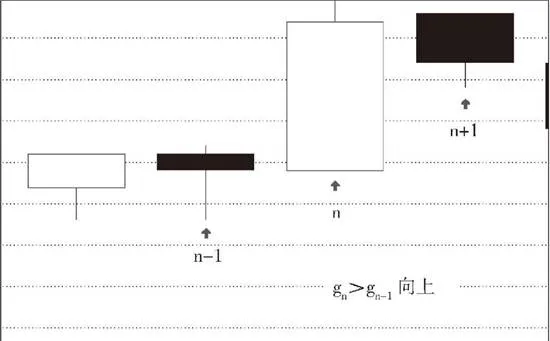
上圖是第n-n、n+1根K線向上關係示意圖
注意,這種定義是唯一的,有統一答案的。就算是本ID如果弄錯了,那也是錯,沒有任何含糊的地方。這個答案與時間無關,與人無關,是客觀的,不可更改的,唯一的要求就是被分析的K線已經走出來。
從這裏可以看出,本ID理論的當下性也就有了一個很客觀的描述。爲什麼要當下的?因爲如果當下那些K線還有沒走出來,那麼具體的分型就找不出來,相應的筆、線段、最低級別中樞、高級別走勢類型等就不可能劃分出來,這樣就無從分析了。
一旦當下的K線走出來,就可以當下按客觀標準唯一地找出相應的分型結構。當下的分析和事後的分析是一樣的,分析的結果也是一樣的,沒有任何的不同。因此當下性就是本ID的客觀性。
有人可能要問,如果看30分鐘圖,K線可能會一直犬牙交錯,找不到分型。這有什麼奇怪的?在年線圖裏,找到分型的機會更小,十幾年找不到一個也很正常,這裏還是用顯微鏡倍數來比喻問題。
確定顯微鏡的倍數,就按看到的K線用定義嚴格地尋找。沒有符合定義的對象,就是確實不存在,就這麼簡單。如果希望能分析得更精確,那就用小級別的圖,這樣自然能分辨得更清楚。
再次強調,用什麼圖與以什麼級別操作沒有任何必然聯繫。用1分鐘圖,也可以找出年線級別的背馳,然後進行相應級別的操作。看1分鐘圖,並不意味着一定要玩超短線。把顯微鏡當成顯微鏡觀察的對象,肯定是不對的。
從分型到筆,必須是一頂一底相連接。那麼兩個頂或底能構成一筆嗎?這裏分兩種情況。
第一種,在兩個頂或底中間有其他的頂和底。這種情況下,只是把好幾筆當成了一筆,只要繼續用一頂一底的原則處理,自然可以解決。
第二種,在兩個頂或底中間沒有其他的頂和底。這種情況意味着第一個頂或底後的轉折級別太小,不足以構成值得考察的對象。這種情況下,第一個頂或底可以忽略不計。
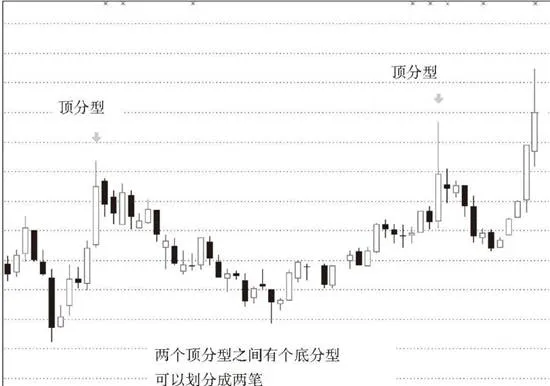
上圖所示爲情況示意圖
根據上面的分析,對第二種情況進行相應處理之後,可以嚴格地說,先頂後底,構成向下一筆;先底後頂,構成向上一筆。所有的圖形,都可以唯一地分解爲上下交替的筆的連接。
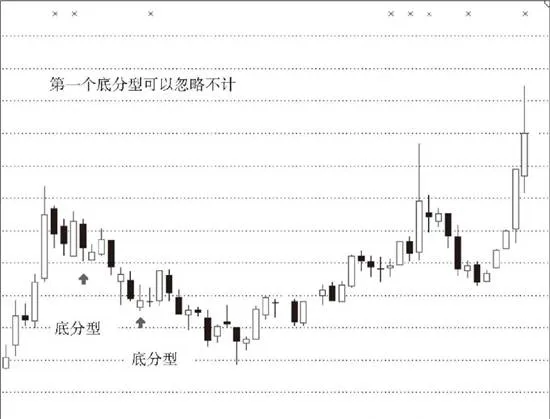
上圖所示爲情況示意圖
顯然,除了第二種情況中的第一個頂或底類似的分型,其他類型的分型,都唯一地分別屬於相鄰的上下兩筆,是這兩筆間的連接。用一個最簡單的比喻,膝蓋就是分型,而大腿和小腿就是連接的兩筆。
有了筆,那麼線段就很簡單了。線段至少有3筆。線段無非有兩種,從向上一筆開始的線段和從向下一筆開始的線段。
對於從向上一筆開始的,其中的分型構成這樣的序列:d1g1,d2g2,d3g3…dngn(其中di代表第i個底,gi代表第i個頂)。如果找到i和j,j≥i+2,使得dj≤gi,那麼稱向上線段被筆破壞。
對於從向下一筆開始的,其中的分型構成這樣的序列:g1d1,g2d2…gndn(其中di代表第i個底,gi代表第i個頂)。如果找到i和j,j≥i+2,使得gj≥di,那麼稱向下線段被筆破壞。
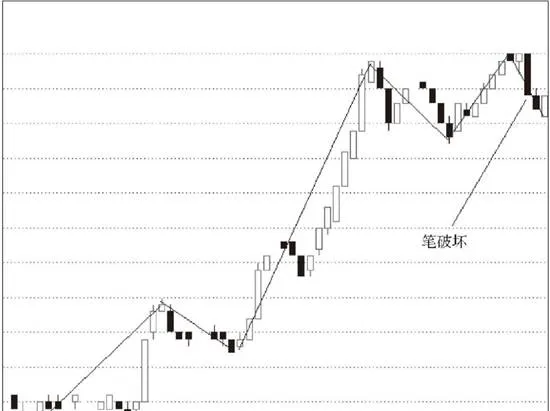
上圖所示爲向上線段被筆破壞示意圖
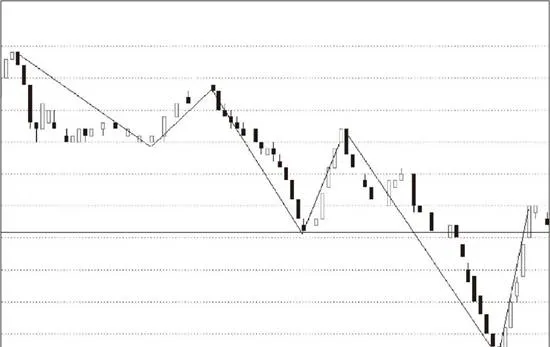
上圖所示爲向下線段被筆破壞示意圖
線段有一個最基本的前提,就是線段的前3筆必須有重疊的部分,這個前提在前面可能沒有特別強調,這裏必須特別強調一次。線段至少有3筆,但並不是連續的3筆就一定構成線段,這3筆必須有重疊的部分。
由上面線段被筆破壞的定義,可以證明纏中說禪線段分解定理:線段被破壞,當且僅當至少被有重疊部分的連續3筆的其中一筆破壞。只要構成有重疊部分的前3筆,那麼必然會形成一段線段。換言之,線段破壞的充要條件,就是被另一個線段破壞。
以上都是些最嚴格的幾何定義。真想把問題搞清楚的人,請自己根據定義多畫圖,或者對照真實的走勢圖用定義多分析。注意,所有分析答案,只和你看的走勢品種與級別圖有關。在客觀地觀照對象與顯微鏡倍數確定的情況下,任何分析都是唯一的,客觀的,不以任何人的意志爲轉移。
如果分型、筆、線段這些最基礎的東西都沒有搞清楚,不能做到在任何時刻,面對任何最複雜的圖形,當下地進行快速正確的分解,就說要掌握本ID的理論,那純粹是瞎掰。
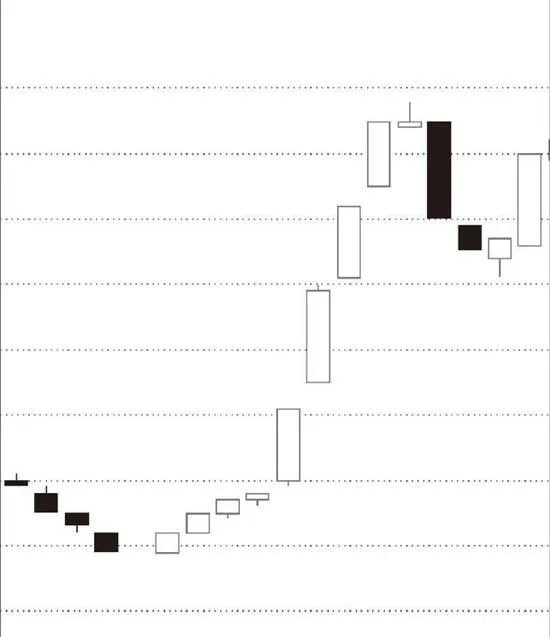
上圖中連續3筆沒有重疊,不構成線段
纏論點睛
1.一筆中間的分型,可以稱作中繼分型。如果一個分型之後的反向力度很弱,那麼該分型就有可能演化爲中繼分型。
2.線段的前3筆必須有重疊,且第一筆和最後一筆的方向一致。也就是說線段中,筆的個數都是奇數且爲大於或等於3的奇數。
投資微言
低級別圖上用中樞、走勢類型,高級別圖上用分型、筆、線段,等於有兩套有用的工具去分析同一走勢,這是天大的好事。