分形維數
歐氏幾何學有着幾千年的歷史,它研究的是一些規整的圖形,如直線、圓、橢圓、菱形、正方形、立方體、長方體、球體等。這些不同類型的曲線和形狀都有一個共同的基礎—歐氏幾何,即它們可以被定義爲代數方程(例如,Ax+By+Cz=D)或微分方程的解集。從歐氏幾何測量中,可以看出點、直線、平面圖形、空間圖形的維數分別是0,1,2和3,而且都是整數。
維數是幾何對象的重要特徵量,維數包含了集合的幾何性質的許多信息。一個圖形維數的大小,表示它佔有空間的大小。尤其是在分形中,它對如何準確地描述圖形起到了很大的作用。分形維數是判斷兩個分形是否一致的度量標準之一。
拓撲維數
在經典幾何學中,維數是形體的一個重要特徵量,即爲了確定幾何形體的每一個點在空間中的位置所需要的獨立座標的數目。在平直的歐氏空間內,形體的維數是顯然的;點是零維的;線是一維的;面是二維的;體是三維的。對點、線、面、體這樣的幾何形體在連續拉伸、壓縮、扭曲等形變下,其對應的維數是不變的,是正整數,我們稱此維數爲拓撲維數。
Hausdorff維數
測量一個幾何形體大小所得到的數值N與形體維數(拓撲維數)和測量的標度(長度單位)l有密切關係。例如:
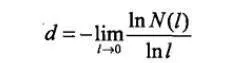
若l足夠小,則上式與l無關。這對任何大小和形狀的幾何體都成立。對通常的幾何體而言,d是整數。1919年,德國數學家豪斯多夫(F.Hausdorff)認爲,可以把上式推廣到維數,則d不一定取整數。人們便將此定義的維數d稱爲豪斯多夫維數,並記爲dH,即:
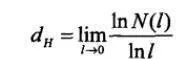
容A維數
豪斯多夫維數的式子是以被測幾何體的容量大小來進行分析計算的,因此通常叫做容量維數,可記爲do,又稱盒維數,記爲db.
相似維數
設幾何體的體積壓縮比爲k,線度壓縮比爲λ,幾何體的維數爲d,則它們之間的關係是:k=λd。
將這一概念推廣應用於分形,由於分形的自相似性,線度變小(縮小)仍將得到與原分形體相似的子集。
設此分形體是由k個與之相似的不相交子集所組成的,於是推廣上式可得:
k=λd或者k=λ-d=1
d是與此分形體的結構有關並有維數特徵的特徵量,稱爲相似維數。
除了以上維數外,還有標度關係、多重分形等關於分形結構的描述。