分形维数
欧氏几何学有着几千年的历史,它研究的是一些规整的图形,如直线、圆、椭圆、菱形、正方形、立方体、长方体、球体等。这些不同类型的曲线和形状都有一个共同的基础—欧氏几何,即它们可以被定义为代数方程(例如,Ax+By+Cz=D)或微分方程的解集。从欧氏几何测量中,可以看出点、直线、平面图形、空间图形的维数分别是0,1,2和3,而且都是整数。
维数是几何对象的重要特征量,维数包含了集合的几何性质的许多信息。一个图形维数的大小,表示它占有空间的大小。尤其是在分形中,它对如何准确地描述图形起到了很大的作用。分形维数是判断两个分形是否一致的度量标准之一。
拓扑维数
在经典几何学中,维数是形体的一个重要特征量,即为了确定几何形体的每一个点在空间中的位置所需要的独立坐标的数目。在平直的欧氏空间内,形体的维数是显然的;点是零维的;线是一维的;面是二维的;体是三维的。对点、线、面、体这样的几何形体在连续拉伸、压缩、扭曲等形变下,其对应的维数是不变的,是正整数,我们称此维数为拓扑维数。
Hausdorff维数
测量一个几何形体大小所得到的数值N与形体维数(拓扑维数)和测量的标度(长度单位)l有密切关系。例如:
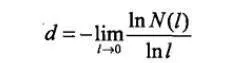
若l足够小,则上式与l无关。这对任何大小和形状的几何体都成立。对通常的几何体而言,d是整数。1919年,德国数学家豪斯多夫(F.Hausdorff)认为,可以把上式推广到维数,则d不一定取整数。人们便将此定义的维数d称为豪斯多夫维数,并记为dH,即:
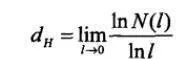
容A维数
豪斯多夫维数的式子是以被测几何体的容量大小来进行分析计算的,因此通常叫做容量维数,可记为do,又称盒维数,记为db.
相似维数
设几何体的体积压缩比为k,线度压缩比为λ,几何体的维数为d,则它们之间的关系是:k=λd。
将这一概念推广应用于分形,由于分形的自相似性,线度变小(缩小)仍将得到与原分形体相似的子集。
设此分形体是由k个与之相似的不相交子集所组成的,于是推广上式可得:
k=λd或者k=λ-d=1
d是与此分形体的结构有关并有维数特征的特征量,称为相似维数。
除了以上维数外,还有标度关系、多重分形等关于分形结构的描述。