纏論第62課:分型、筆與線段
本ID的線段是可以精確定義的。本ID的理論,本質上是一套幾何理論,其有效性就如同幾何一般。當然本ID理論有失敗和不嚴謹的時候,但前提是幾何的基礎失敗和不嚴謹,不明白這一點,就不明白本ID的理論。
下面的定義與圖,適合任何週期的K線圖。圖中的小線段代表的是K線,這裏不分陽線陰線,只看K線高低點。
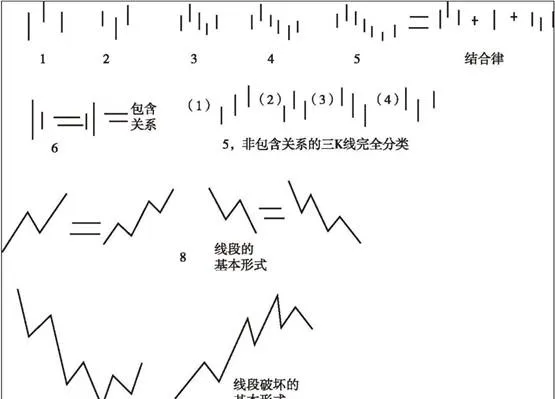
上圖所示爲基本的分型、筆、線段示意圖
像上圖這種,第二根K線高點是相鄰三根K線高點中最高的,而低點也是相鄰三根K線低點中最高的,本ID給出一個定義叫頂分型。小圖2這種叫底分型,第二根K線低點是相鄰三根K線低點中最低的,而高點也是相鄰三根K線高點中最低的。
頂分型的最高點叫該分型的頂,底分型的最低點叫該分型的底。由於頂分型的底和底分型的頂是沒有意義的,所以頂分型的頂和底分型的底可以簡稱爲頂和低。也就是說,當我們以後說頂和底時,就是分別說頂分型的頂和底分型的底。
兩個相鄰的頂和底之間構成一筆。一筆內部的波動都可以忽略不計。但注意,一定是相鄰的頂和底才構成一筆,隔了幾個就不是了。
所謂的線段,至少由3筆組成。這裏有一個細微的地方要分清楚,因爲結合律是必須遵守的。像小圖3這種,頂和底之間共用一根K線,這就違反結合律了,所以不算一筆。小圖4中只有頂和底,中間沒有其他K線,一般來說,也最好不算一筆。
圖小圖5中頂和底之間還有一根K線,是一筆的最基本圖形。在實際分析中,要求頂和底之間至少有一根K線,才能當成是一筆。
實際的圖形裏,會出現一些複雜的關係,就是相鄰兩K線之間可以出現如小圖6這種包含關係,也就是一根K線的高低點全在另一根K線的範圍裏。
這種情況可以這樣處理:在向上時,把兩根K線的最高點當高點,而兩根K線低點中的較高者當成低點,這樣就把兩根K線合併成一根新的K線;反之,當向下時,把兩根K線的最低點當低點,而兩根K線高點中的較低者當成高點,這樣就把兩根K線合併成一根新的K線。經過這樣的處理,所有K線圖都可以處理成沒有包含關係的圖形。
小圖7給出了經過以上處理,沒有包含關係的圖形中3根相鄰K線之間可能組合的一個完全分類,其中的(2)、(3),分別是頂分型和底分型。(1)可以叫做上升K線,(3)可以叫做下降K線。
由結合律,上升的一筆一定是底分型+上升K線+頂分型;下降的一筆,一定是頂分型+下降K線+底分型。注意,這裏的上升、下降K線,不一定都是3根,可以是無數根。簡單的,也可以是一兩根,只要一直符合定義就可以。
至於小圖8,就是線段的最基本形態。小圖9就是線段破壞,也就是兩線段組合的其中一種形態。
有人可能會說,這怎麼有點像波浪理論?這有什麼奇怪的,本ID的理論可以嚴格地推導出波浪理論的所有結論,而且還可以指出其不足的地方,波浪理論和本ID的理論一點可比性都沒有。不僅是波浪理論,所有關於股市的理論,只要是涉及到圖形的,本ID的理論都可以嚴格推論,因爲本ID的理論是關於走勢圖形最基礎的理論,誰都逃不掉。
纏論點睛
1.K線非包含處理的方法:向上筆中,高點中較高的作爲高點,低點中較高的作爲低點;向下筆中,低點中較低的作爲低點,高點中較低的作爲高點。所有K線按照時間順序進行非包含處理。
2.任何週期的K線,經過非包含處理之後,都可以標準化爲只包含頂分型、底分型、上升K線、下降K線等四種基本形態的圖形。
3.在後面的課程中,一頂一底的連接可以算作一筆,中間可以不包含K線。
4.線段只有被新的線段破壞纔算結束。當然,也可以用背馳以及盤整背馳的方法分析線段內部,用以判斷線段的結束點。
投資微言
可以直接用分型、筆、線段對某級別進行分析,這是纏論形態學的內容。