什么是线性回归?
线性回归是一种数据分析,它考虑因变量与一个或多个自变量之间的线性关系。它通常用于直观地显示各种因素之间关系或相关性的强度以及结果的离散性——所有这些都是为了解释因变量的行为。线性回归模型的目标是估计变量之间关系的大小以及它是否具有统计显著性。
假设我们想测试冰淇淋的摄入量与肥胖之间的关系强度。我们将冰淇淋的摄入量作为独立变量,并将其与肥胖作为因变量联系起来,看看是否存在关系。鉴于回归是这种关系的图形显示,数据的变异性越低,关系越强,回归线的拟合度就越高。
在金融领域,线性回归用于确定资产价格与经济数据之间的关系,应用范围广泛。例如,它用于确定Fama-French 模型中的因子权重,并且是确定资本资产定价模型(CAPM) 中股票贝塔系数的基础。
在这里,我们研究如何使用导入到 Microsoft Excel 的数据执行线性回归以及如何解释结果。
重点摘要
- 线性回归模拟因变量和自变量之间的关系。
- 线性回归也称为普通最小二乘法 (OLS),本质上是估计模型中所有变量之间的最佳拟合线。
- 如果变量是独立的,不存在异方差,并且变量的误差项不相关,则可以认为回归分析是稳健的。
- 使用数据分析工具库可以更轻松地在 Excel 中建立线性回归模型。
- 回归输出可以解释为因变量上一个或多个变量之间的相关性的大小和强度。
重要注意事项
要进行回归分析,必须对数据集做出几个关键假设。否则,结果将被错误解释或出现偏差:
如果这三点听起来很复杂,那确实如此。但如果其中一个考虑因素不成立,就会导致估计有偏差。本质上,你会错误地陈述你正在衡量的关系。
在 Excel 中输出回归
在 Excel 中运行回归分析的第一步是仔细检查是否安装了免费的 Excel 插件数据分析工具库。此插件使计算一系列统计数据变得非常容易。它不需要绘制线性回归线,但它使创建统计表变得更简单。要验证是否已安装,请从工具栏中选择“数据”。如果“数据分析”是一个选项,则该功能已安装并可供使用。如果未安装,您可以通过单击 Office 按钮并选择“Excel 选项”来请求此选项。
使用数据分析工具库,只需单击几下即可创建回归输出。
Excel 中的独立变量处于 X 范围内。
假设我们想知道,给定标准普尔 500 指数的回报,我们是否可以估计 Visa ( V )股票回报的强度和关系。Visa (V) 股票回报数据填充第 1 列作为因变量。标准普尔 500 指数回报数据填充第 2 列作为自变量。
- 从工具栏中选择“数据”。显示“数据”菜单。
- 选择“数据分析”。显示“数据分析 - 分析工具”对话框。
- 从菜单中选择“回归”,然后单击“确定”。
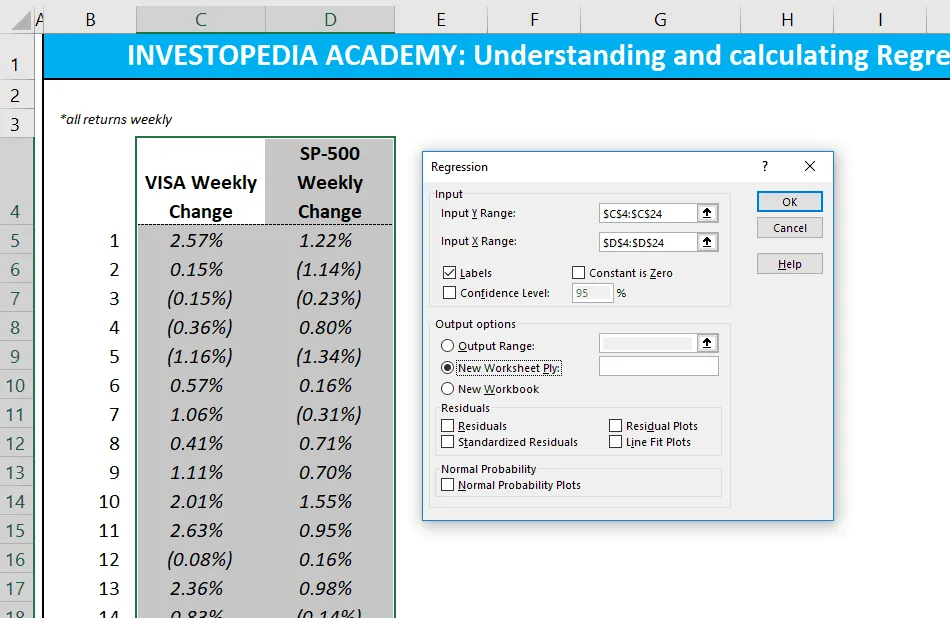
- 在回归对话框中,单击“输入 Y 范围”框并选择因变量数据(Visa(V)股票收益)。
- 单击“输入X范围”框并选择独立变量数据(标准普尔500指数回报)。
- 单击“确定”运行结果。
[注意:如果表格看起来很小,请右键单击图像并在新选项卡中打开以获得更高的分辨率。]
解释结果
使用该数据(与我们的R 平方文章相同),我们得到下表:
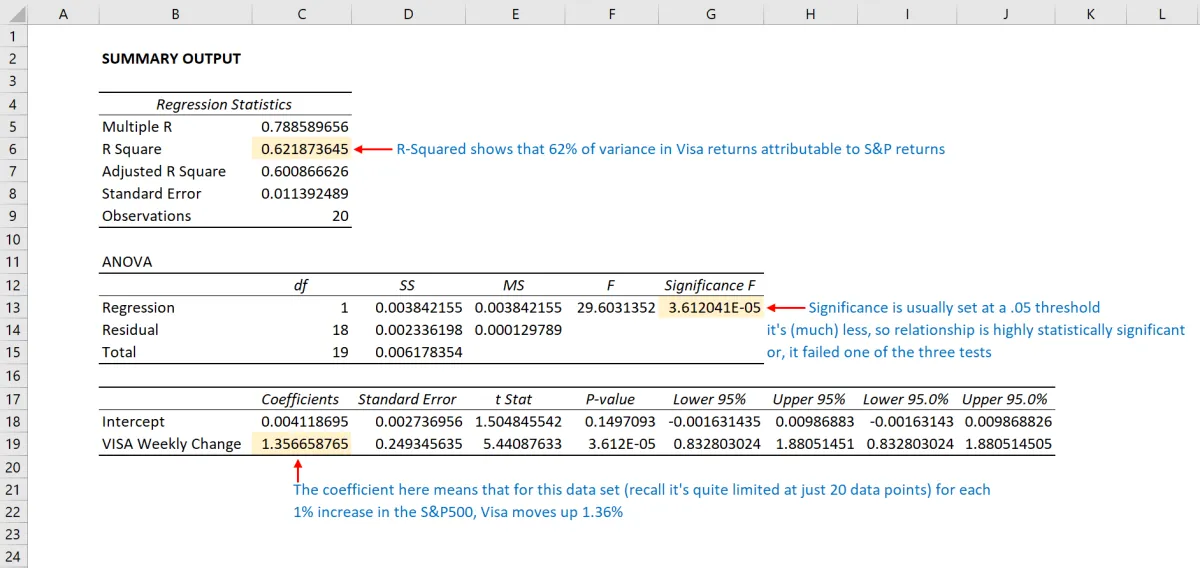
R 2值,也称为判定系数,用于测量自变量解释因变量变异的比例,或回归模型与数据的拟合程度。R 2值的范围为 0 到 1,值越大表示拟合度越高。p 值或概率值的范围也为 0 到 1,表示检验是否显著。与 R 2值相比,p 值越小越有利,因为它表示因变量和自变量之间存在相关性。
解释结果
这里的底线是 Visa 股票的变化似乎与标准普尔 500 指数高度相关。
- 在上面的回归输出中,我们可以看到 Visa 每变化 1 个点,标准普尔 500 指数就会相应变化 1.36 个点。
- 我们还可以看到 p 值非常小(0.000036),这也对应于非常大的 T 检验。这表明这一发现具有高度的统计显著性,因此这一结果由偶然因素造成的可能性极低。
- 从 R 平方我们可以看出,仅 V 价格就能解释标准普尔 500 指数中 62% 以上的波动。
然而,分析师此时可能会出于以下原因而保持谨慎:
在 Excel 中绘制回归图表
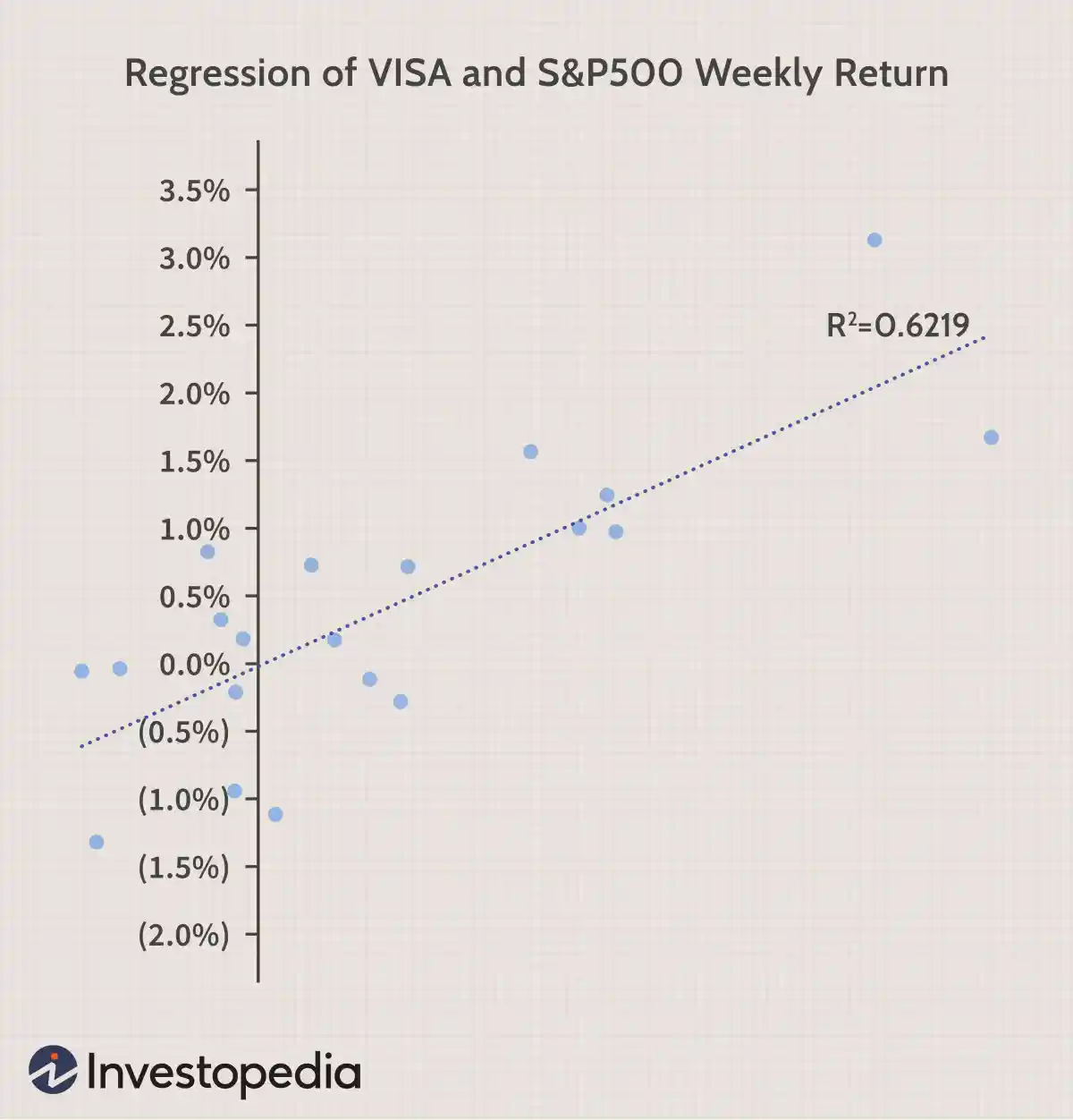
我们可以在 Excel 中通过突出显示数据并将其绘制为散点图来绘制回归图。要添加回归线,请从“图表工具”菜单中选择“布局”。在对话框中,选择“趋势线”,然后选择“线性趋势线”。要添加 R 2值,请从“趋势线”菜单中选择“更多趋势线选项”。最后,选择“在图表上显示 R 平方值”。视觉结果总结了关系的强度,尽管其代价是没有提供上表那么多细节。
如何解释线性回归?
回归模型的输出将产生各种数值结果。系数(或 beta 值)告诉您其他所有变量保持不变的情况下独立变量与因变量之间的关联。如果系数为 +0.12,则表示该变量每变化 1 个点,因变量就会在同一方向上变化 0.12 个点。如果系数为 -3.00,则意味着解释变量变化 1 个点,因变量就会在相反方向上变化 3 倍。
如何知道回归是否显著?
如何解释线性回归的 R 平方?
R 2 ( R 平方) 是线性回归模型拟合优度的统计量度(从 0.00 到 1.00),也称为判定系数。一般而言,R 2越高,模型拟合度越高。R 平方也可以解释为因变量的变化中有多少是由模型中的独立(解释)变量解释的。因此,R 平方为 0.50 表示因变量中观察到的所有变化中有一半可以由因变量解释。