什麼是線性迴歸?
線性迴歸是一種數據分析,它考慮因變量與一個或多個自變量之間的線性關係。它通常用於直觀地顯示各種因素之間關係或相關性的強度以及結果的離散性——所有這些都是爲了解釋因變量的行爲。線性迴歸模型的目標是估計變量之間關係的大小以及它是否具有統計顯著性。
假設我們想測試冰淇淋的攝入量與肥胖之間的關係強度。我們將冰淇淋的攝入量作爲獨立變量,並將其與肥胖作爲因變量聯繫起來,看看是否存在關係。鑑於迴歸是這種關係的圖形顯示,數據的變異性越低,關係越強,迴歸線的擬合度就越高。
在金融領域,線性迴歸用於確定資產價格與經濟數據之間的關係,應用範圍廣泛。例如,它用於確定Fama-French 模型中的因子權重,並且是確定資本資產定價模型(CAPM) 中股票貝塔係數的基礎。
在這裏,我們研究如何使用導入到 Microsoft Excel 的數據執行線性迴歸以及如何解釋結果。
概要
- 線性迴歸模擬因變量和自變量之間的關係。
- 線性迴歸也稱爲普通最小二乘法 (OLS),本質上是估計模型中所有變量之間的最佳擬合線。
- 如果變量是獨立的,不存在異方差,並且變量的誤差項不相關,則可以認爲迴歸分析是穩健的。
- 使用數據分析工具庫可以更輕鬆地在 Excel 中建立線性迴歸模型。
- 迴歸輸出可以解釋爲因變量上一個或多個變量之間的相關性的大小和強度。
重要注意事項
要進行迴歸分析,必須對數據集做出幾個關鍵假設。否則,結果將被錯誤解釋或出現偏差:
如果這三點聽起來很複雜,那確實如此。但如果其中一個考慮因素不成立,就會導致估計有偏差。本質上,你會錯誤地陳述你正在衡量的關係。
在 Excel 中輸出迴歸
在 Excel 中運行迴歸分析的第一步是仔細檢查是否安裝了免費的 Excel 插件數據分析工具庫。此插件使計算一系列統計數據變得非常容易。它不需要繪製線性迴歸線,但它使創建統計表變得更簡單。要驗證是否已安裝,請從工具欄中選擇“數據”。如果“數據分析”是一個選項,則該功能已安裝並可供使用。如果未安裝,您可以通過單擊 Office 按鈕並選擇“Excel 選項”來請求此選項。
使用數據分析工具庫,只需單擊幾下即可創建迴歸輸出。
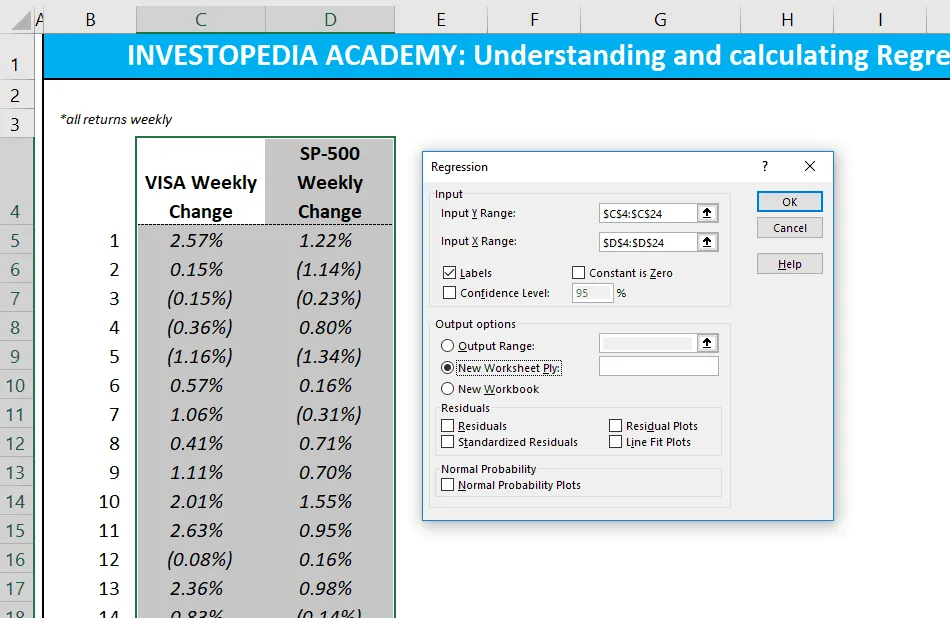
Excel 中的獨立變量處於 X 範圍內。
假設我們想知道,給定標準普爾 500 指數的回報,我們是否可以估計 Visa ( V )股票回報的強度和關係。Visa (V) 股票回報數據填充第 1 列作爲因變量。標準普爾 500 指數回報數據填充第 2 列作爲自變量。
- 從工具欄中選擇“數據”。顯示“數據”菜單。
- 選擇“數據分析”。顯示“數據分析 - 分析工具”對話框。
- 從菜單中選擇“迴歸”,然後單擊“確定”。
- 在迴歸對話框中,單擊“輸入 Y 範圍”框並選擇因變量數據(Visa(V)股票收益)。
- 單擊“輸入X範圍”框並選擇獨立變量數據(標準普爾500指數回報)。
- 單擊“確定”運行結果。
[注意:如果表格看起來很小,請右鍵單擊圖像並在新選項卡中打開以獲得更高的分辨率。]
解釋結果
使用該數據(與我們的R 平方文章相同),我們得到下表:
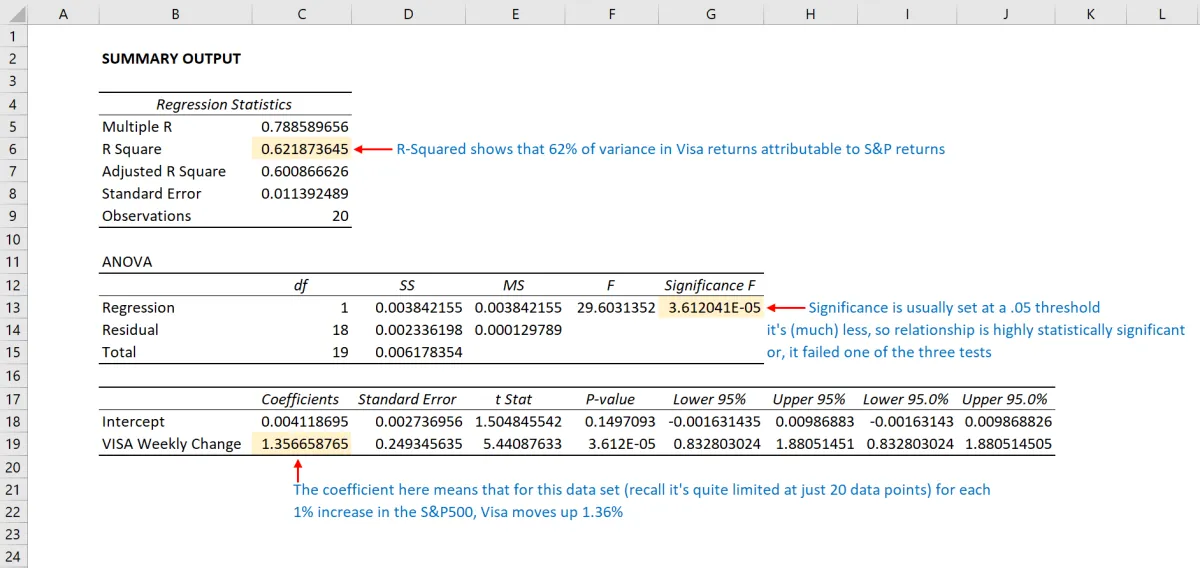
R 2值,也稱爲判定係數,用於測量自變量解釋因變量變異的比例,或迴歸模型與數據的擬合程度。R 2值的範圍爲 0 到 1,值越大表示擬合度越高。p 值或概率值的範圍也爲 0 到 1,表示檢驗是否顯著。與 R 2值相比,p 值越小越有利,因爲它表示因變量和自變量之間存在相關性。
解釋結果
這裏的底線是 Visa 股票的變化似乎與標準普爾 500 指數高度相關。
- 在上面的迴歸輸出中,我們可以看到 Visa 每變化 1 個點,標準普爾 500 指數就會相應變化 1.36 個點。
- 我們還可以看到 p 值非常小(0.000036),這也對應於非常大的 T 檢驗。這表明這一發現具有高度的統計顯著性,因此這一結果由偶然因素造成的可能性極低。
- 從 R 平方我們可以看出,僅 V 價格就能解釋標準普爾 500 指數中 62% 以上的波動。
然而,分析師此時可能會出於以下原因而保持謹慎:
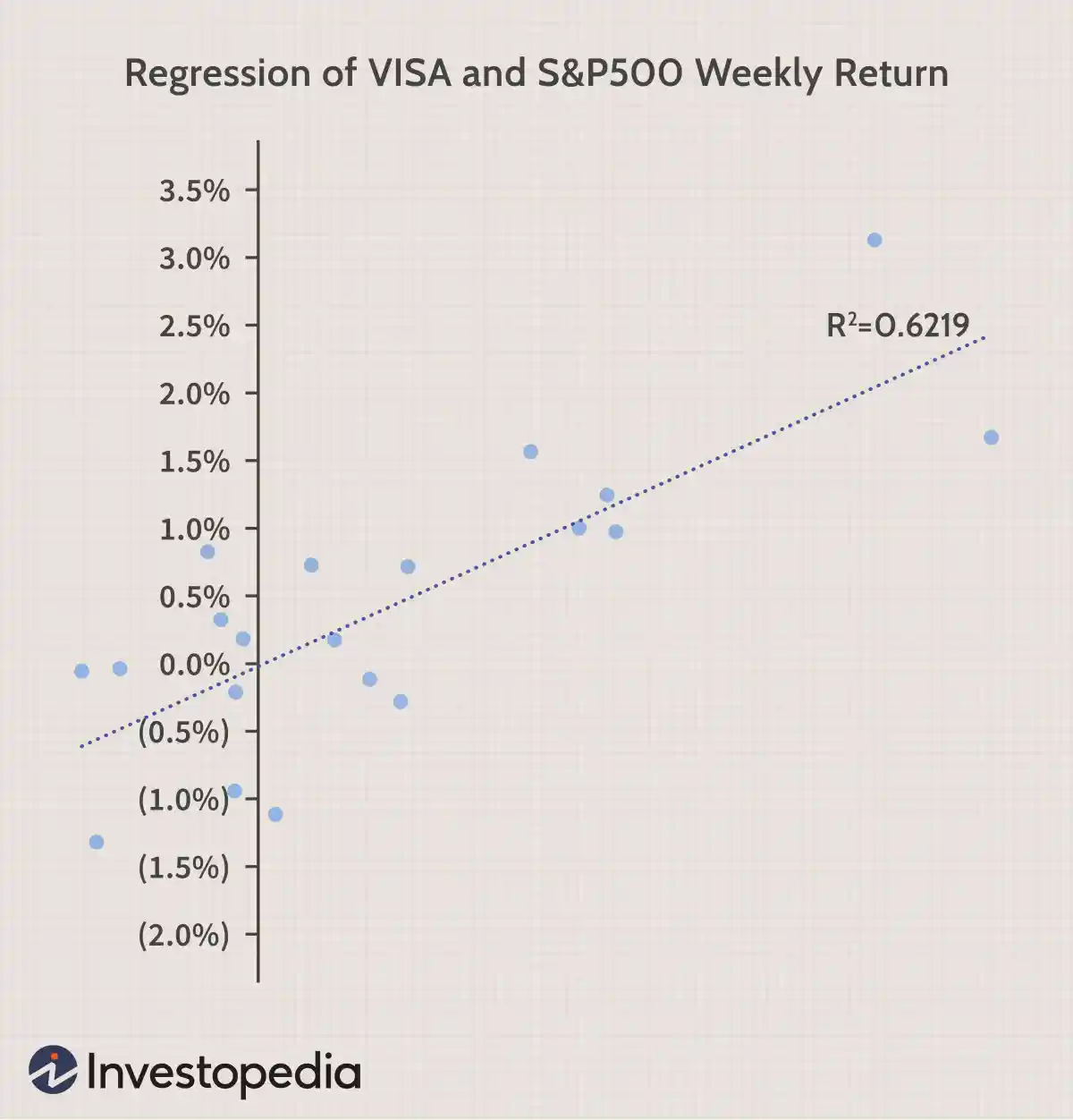
在 Excel 中繪製迴歸圖表
我們可以在 Excel 中通過突出顯示數據並將其繪製爲散點圖來繪製迴歸圖。要添加回歸線,請從“圖表工具”菜單中選擇“佈局”。在對話框中,選擇“趨勢線”,然後選擇“線性趨勢線”。要添加 R 2值,請從“趨勢線”菜單中選擇“更多趨勢線選項”。最後,選擇“在圖表上顯示 R 平方值”。視覺結果總結了關係的強度,儘管其代價是沒有提供上表那麼多細節。
如何解釋線性迴歸?
迴歸模型的輸出將產生各種數值結果。係數(或 beta 值)告訴您其他所有變量保持不變的情況下獨立變量與因變量之間的關聯。如果係數爲 +0.12,則表示該變量每變化 1 個點,因變量就會在同一方向上變化 0.12 個點。如果係數爲 -3.00,則意味着解釋變量變化 1 個點,因變量就會在相反方向上變化 3 倍。
如何知道迴歸是否顯著?
如何解釋線性迴歸的 R 平方?
R 2 ( R 平方) 是線性迴歸模型擬合優度的統計量度(從 0.00 到 1.00),也稱爲判定係數。一般而言,R 2越高,模型擬合度越高。R 平方也可以解釋爲因變量的變化中有多少是由模型中的獨立(解釋)變量解釋的。因此,R 平方爲 0.50 表示因變量中觀察到的所有變化中有一半可以由因變量解釋。