案例:基於小波分析的金觸時序數據預側
1)實驗步驟
利用Mtlab軟件,對金融數據的預測可以按以下步驟進行。
(1)對原始數據進行分解,本案例採用Mallat算法對數據進行分解,然後對信號進行平滑處理,用低通函數與原始信號卷積實現平滑處理,然後對經過平滑處理的信號進行重構。
(2)檢驗處理後的數據是否符合AR[p]建模要求,計算自相關係數x,x=R/R0,其中R0爲自協方差函數。
(3)通過求解Y-W方程,求得偏相關函數X。
(4)計算10階以內的模型殘差方差U和AIC值,應用AIC準則爲模型定階,AIC準則:
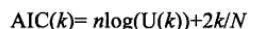
(5)檢驗{at}是否爲白噪聲,求{at}的自相關係數P,看其是否趨近於零,若趨近於零,模型適用;否則,模型不適用。
(6)本案例中判定模型階數爲7,利用AR[7]模型的方程對重構後的數據進行預測,AR[7]模型方程爲:
X(t)=W(1)×X(t-1)-W(2)×X(t-2)-W(3)×X(t-3)-W(4)×X(t-4)-W(5)×X(t-5)-W(6)×X(t-6)-W(7)xX(t-7)+a
2)實證結果
本案例取深發展A股股票2005年1月4日到2005年12月30日的每交易日的收盤價格(共有227個交易日)作爲已知時刻的值,用上述小波變換的方法來預測2006年1月1日到2006年1月7日的6個交易日的股票收盤價的值,並與實際值相比較。
首先給出原始數據圖,如圖12-4所示,對上述數據用小波進行分解,並對分解後的數據做平滑處理,然後重構得到原數據的近似信號,這時數據走勢如圖12-5所示。
通過比較可以看出,進行小波變換後,時間序列趨於平穩,我們將其看做原始數據的近似信號,利用AR[7]模型對原始數據的近似信號進行逼近,時間區間爲2006/1/1-2006/1/7,共有6個交易日的原始數據,結果如表12-1所示。從表中可以看到,預測的總體趨勢和實際股票價格的走勢一致,預測的效果很好。
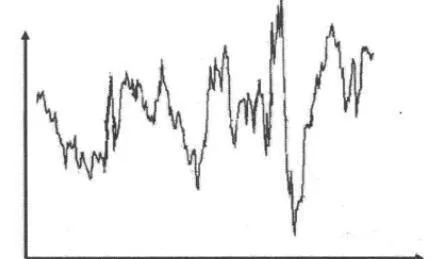
圖12-4 深發展A股票收盤價2005年227個交易日的股價走勢
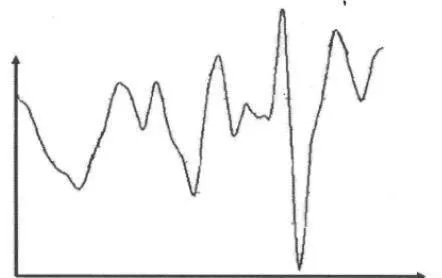
圖12-5 深發展A小波重構

表12-1 深發展A日收盤價小波分析方法預測值與實際值比較
在小波分析預測方法中,還存在分解層數的問題。小波越往下分解,信號頻段劃分得越細,細節信號和近似信號的平穩性就越好,這樣預測值會比較精確。但實際上,由於分解過程中本身存在計算的誤差,層數越多,誤差就會越大,這樣這種誤差就會影響預測值。因此在選擇層數時不宜過多,也不宜過少。表12-2給出了採用小波分析方法進行預測時,分解層數分別爲1-6層時的預測誤差均方根值。

表12-2 不同分解層數的誤差均方根值
通過以上案例實證,可以看到小波預測方法在預測處理金融數據這類非平穩的時間序列時,預測的結果與實際值很接近,效果較好。雖然所預測的結果仍會出現個別偏大或者偏小的值,但是可以看出小波方法預測的效果同傳統的預測方法相比較,其具有一定的可靠性,用於預測股價的短期(六、七天)走勢,效果比較好。同時也可以發現,一般當分解層數在2~3層時,預測效果比較好。