開始本章節之前,我們還是回憶一下。“數量化算法對於數據的種類是否有明確的要求?”答案是否定的。如果願意,讀者可以使用宏觀經濟類數據、行業公司數據、二級市場數據。它也剛好說明了常見的三種分析邏輯和手段。
有首席經濟學家說:“目前主流的股市預測一般都通過對經濟週期的判斷來預測股市”。這話至少在筆者的工作層面得到了證實。有一段時間,筆者和幾位同事總是聽到“朱格拉週期”、“變頻”、“疊加”這種東西,以至於某同事私下聊天時還不忘調侃一下。
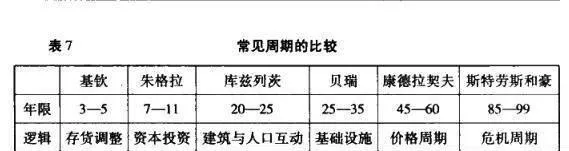
表7常見週期的比較
由於週期背後的邏輯關係不相同,一般來說很少會各個週期的低點同時出現,產生較爲嚴重的共振影響。比如,普盧默就在其《金融市場預測》一書中指出:“並非康德拉契夫週期中所有的低點都是大蕭條,因爲,並非所有的斯特勞斯和豪週期的低點與康德拉契夫週期的低點相吻合。”
筆者本身對這個領域的興趣並不高,部分原因在於某首席經濟學家指出的兩個不確定性:“一是你能否準確預測經濟波動的方向、拐點與走勢,二是你能否預測經濟波動將對股市走勢產生怎樣的影響。單純看這兩個環節,對於股市變化方向判斷的平均準確率就只有25%,更何況你還要.判斷漲跌區間、描述走勢圖,則準確率就更低了。況且中國股市與經濟走勢的關聯度從歷史,上看並不大,還有諸多影響股市的因素是很難量化的,這就使得預測股市走勢幾乎不可能。”
另外,武康平教授的《高級宏觀經濟學》中,在第二章經濟週期理論裏也談到了這一點:“這種沒有簡單規律的波動,可謂是宏觀經濟短期波動的一個突出特點。也正是基於這一事實,當代宏觀經濟學才放棄了過去那種力圖把經濟週期解釋爲具有某種規則性的週期的做法,比如,放棄了過去那種解釋爲基欽週期、朱格拉週期、庫茲列茨週期、康德拉契夫週期的傳統做法,也放棄了過去那種力圖通過各種長度不同的確定性週期的組合來解釋和說明經濟波動現象的做法。之所以放棄,是因爲過去的這些理論對於解釋當代經濟波動現象機會沒有多大用處。”當然,這還沒有涉及從經濟走勢到股市走勢的問題。
另一種思路是通過部分經濟指標來考察股市問題。貨幣供應、信貸投放和CPI、PPI剪刀差等都曾經出現過。筆者對這一思路的態度是肯定的。因爲這是一個邏輯和實證都能講得通的領域。所以筆者傾向認爲採用部分經濟指標作爲算法設計的依託是可行的。
行業公司數據是被研究機構挖掘最多的領域,不用筆者多談。這也是普遍被認爲存在利用價值的領域。但如果數據頻率過低,就難免會有較大的風險。二級市場數據是爭議最大的一個部分。其中一個可以理解的原因在於走勢的相關性究竟要如何體現。普盧默用道瓊斯工業平均指數1天的百分比變動和5天的百分比變動試圖說明一個問題:“分析的時間段越長,波動的幅度就越可能缺乏隨機性。”擺在我們面前的疑問是,A股市場又如何呢?這個對比並不復雜,排除異常值對於結果沒有什麼實質影響。下圖就是當漲跌幅分別取1. 5、20三個參數所得到的結果。我們得到了與普盧默類似的圖形結論。但如果就此認爲“短期的指數變動是較難理出頭緒的,但隨着時間參數的改變,一種模式可能會產生於數據中”卻未免有些牽強。筆者用EXCEL的隨機數函數生成的20000個分佈於-1一1的數值,用類似的參數也能表現出良好的線性關係。當方差出現相應放大的情況下,單獨一日的數據影響程度下降。這對於此類構造方式提供了一個公共部分。數據段除了首尾不同,其餘皆相同的處境自然而然能帶來高線性相關的結果。至於這到底是不是因爲所謂的奇異吸引子,筆者愚以爲也沒必要再去細究了。反過來重新想想這一事例所暴露的問題纔是必要的。一個人的能力是有限的,即便是思維再縝密的人也難免犯錯。如果管理的資金有限,犯錯往往還沒有什麼很大的後果。如果管理的資金過於龐大,則團隊式的協作十分重要,畢竟任何一個錯誤都可能是龐大的賬面損失。
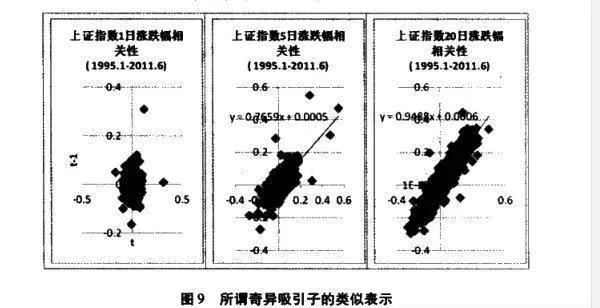
圖9所謂奇異吸引子的類似表示
簡單的總結過後,我們發現經濟類、行業公司類乃至二級市場類數據都可以作爲數量化分析手段的應用。讀者可能就此產生疑感:“三種分析手段都適用,那這數量化到底算是個什麼方法?”坦白說,筆者也很難在這樣的層面上把它歸結爲任何一種。但很顯然,只要是能夠被數量化的分析手段,納入其中就沒什麼根本障礙,它也不會對任何人的投資理念產生本質的衝擊。強調交易紀律,不在“預期”中投資可能纔是數量化的根本。