與傳統的神經網絡方法相比,支持向量機具有更出色的性能,它採用結構風險最小化原則,能在經驗風險與模型複雜度之間做適當的折中,從而獲得更好的推廣能力。但是,支持向量機在實際應用中,關於參數選擇的問題仍然沒有得到很好的解決,如多項式學習機器的階數問題、徑向基機器中的函數寬度,以及Sigmoid機器中函數的寬度和偏移等。統計學習理論目前對這些問題給出了一些建議和解釋,但還沒有給出實際可行的方案,目前也只有通過實驗方法來確定最佳參數。因此,在使用支持向量機進行分類和預測時,如何選擇適當的參數就成了一個非常重要的問題。
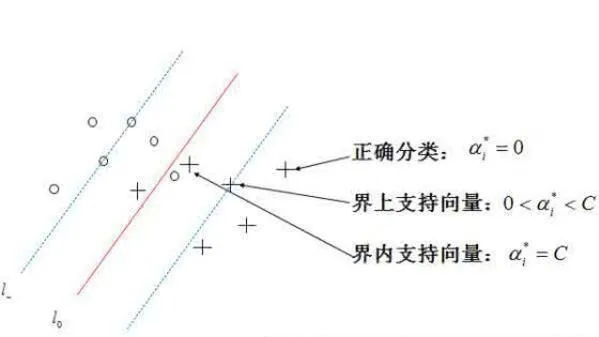
由SVM基本算法可以看出,支持向量機判決函數的依據是支持向量機和偏移值,而支持向量是由訓練集中的一部分組成的,不同的訓練集中訓練出來的支持向 量和偏移是不一樣的,所以SVM分類器性能對訓練集數據選取很敏感。爲了提高支持向最機的分類性能,通常需要不斷調整訓練集,並對其進行多次反覆的訓練,對一個具體分類器找到最佳訓練集,即找到分類中用於判別的支持向量,這就是系統的再學習過程。爲了選擇一個SVM分類器較優的參數,前提是要確定一個好的訓練集。比較常用的方法是先用訓練集一部分樣本訓練,通過實驗得到SVM對這個訓練集的最佳參數,找出對這個訓練集中分類錯誤的樣本,這時把這些分類錯誤的樣本再加到訓練集中,重新使用新的樣本集訓練測試SVM,一直到最佳參數。若分類結果不滿意再重複上述過程。
對於確定的訓練樣本集,研究表明支持向量機RBF核具有較爲優越的性能,所以實驗中通常選擇RBF核函數。RBF核函數實驗中需要調試的參數是懲罰係數C和徑向基寬度σ,關於這兩個參數的選擇,使用交叉選擇的方法可以快速達到最優解。一般來說,C的取值一般爲2 9>C>2 1, or的取值一般小於2 8>σ> 2 1,所以可以先把C的值確定爲9個,即份(2 1,2 2...,2 9),同樣σ的值確定爲8個,這樣再根據經驗選擇以上組合,可以快速達到較優的結果。可以先確定其中一個值,然後微調另一個值,得到分類結果,調好一個參數後再固定它,微調另一個參數,直到達到最佳。