什麼是有效邊界?
有效邊界是一組最優投資組合,這些投資組合在規定的風險水平下提供最高預期回報,或在給定的預期回報水平下提供最低風險。位於有效邊界以下的投資組合是次優的,因爲它們不能爲風險水平提供足夠的回報。聚集在有效邊界右側的投資組合是次優的,因爲它們對定義的回報率具有更高的風險水平。
重點
- 有效邊界包括爲特定風險水平提供最高預期回報的投資組合。
- 投資組合回報的標準差衡量投資風險和投資收益的一致性。
- 投資組合證券之間的較低協方差導致較低的投資組合標準差。
- 回報與風險範式的成功優化應該將投資組合置於有效邊界線上。
- 包含有效邊界的最優投資組合通常表現出更高程度的多樣化。
瞭解有效邊界
有效前沿理論由諾貝爾獎獲得者哈里馬科維茨於 1952 年提出,是現代投資組合理論(MPT) 的基石。有效前沿利率投資組合(投資)在回報(y 軸)與風險(x 軸)的比例上。投資的複合年增長率(CAGR) 通常用作回報成分,而標準差(年化)描述風險指標。
有效邊界以圖形方式表示爲承擔的風險最大化回報的投資組合。 回報取決於構成投資組合的投資組合。證券的標準偏差是風險的同義詞。理想情況下,投資者尋求用提供超常回報但綜合標準差低於單個證券標準差的證券來填充投資組合。
證券同步性越低(協方差越低),標準差越低。如果這種優化回報與風險範式的組合成功,那麼該投資組合應該沿着有效邊界線排列。
該概念的一個關鍵發現是有效邊界的曲率導致多樣化的好處。曲率對於揭示多元化如何改善投資組合的風險/回報狀況是不可或缺的。它還揭示了風險的邊際收益遞減。
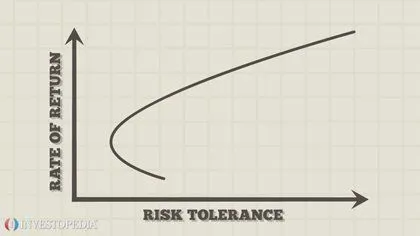
爲投資組合增加更多風險並不會獲得等量的回報——包含有效邊界的最優投資組合往往比次優組合具有更高的多元化程度,次優投資組合通常多元化程度較低。
對有效邊界的批評
有效邊界和現代投資組合理論有許多假設可能無法恰當地代表現實。例如,假設之一是資產收益服從正態分佈。
實際上,證券的回報率(也稱爲尾部風險)可能與均值相差超過三個標準差。因此,據說資產回報遵循尖峯分佈或重尾分佈。
此外,馬科維茨在他的理論中提出了幾個假設,例如投資者是理性的並儘可能避免風險,沒有足夠的投資者來影響市場價格,以及投資者可以無限制地以無風險利率借入和借出資金速度。
然而,現實證明,市場中既有非理性和冒險的投資者,也有影響市場價格的龐大市場參與者,也有不能無限借貸的投資者。
特別注意事項
投資的一個假設是,更高程度的風險意味着更高的潛在回報。相反,承擔低風險的投資者的潛在回報率較低。根據 Markowitz 的理論,存在一個最優投資組合,可以設計爲在風險和回報之間達到完美的平衡。
最優投資組合不僅僅包括具有最高潛在回報的證券或低風險證券。最優投資組合旨在平衡具有最大潛在回報的證券和可接受的風險程度或具有最低風險程度的給定潛在回報水平的證券。最優投資組合所在的風險與預期回報圖上的點稱爲有效邊界。
假設一個尋求風險的投資者使用有效邊界來選擇投資。投資者會選擇位於有效邊界右端的證券。有效邊界的右端包括預期具有高風險和高潛在回報的證券,適合高風險承受能力的投資者。相反,位於有效邊界左端的證券適合規避風險的投資者。
爲什麼有效邊界很重要?
有效邊界以圖形方式描述了多元化的好處。有效邊界的曲率顯示了多元化如何改善投資組合的風險與回報概況。
什麼是最佳投資組合?
最佳投資組合是一種在風險和回報之間達到完美平衡的投資組合。最佳投資組合旨在平衡提供最大可能回報和可接受風險的證券或在給定一定回報的情況下風險最低的證券。
有效邊界是如何構建的?
座標平面上的有效邊界利率投資組合。繪製在 x 軸上的是風險,而繪製在 y 軸上的是回報——年化標準差通常用於衡量風險,而複合年增長率 (CAGR) 用於衡量回報。
投資者如何使用有效邊界?
爲了使用有效邊界,尋求風險的投資者選擇落在邊界右側的投資。與此同時,更保守的投資者會選擇位於邊界左側的投資。