利率變化影響整體經濟、股票市場、債券市場和其他金融市場,並能影響宏觀經濟因素。利率的變化也會影響期權估值,這是一項涉及多種因素的複雜任務,包括標的資產的價格、行權或執行價格、到期時間、無風險回報率(利率)、波動性和股息收益率。除執行價格外,所有其他因素都是未知變量,在期權到期之前都可能發生變化。
定價選項的利率是多少?
瞭解定價選項中使用的正確到期利率非常重要。大多數期權估值模型(例如布萊克-斯科爾斯)都使用年化利率。
如果生息賬戶每月支付 1%,您將獲得 1%*12 個月 = 12% 的年利息。正確的?
不!不同時間段內的利率轉換的工作方式與簡單的時間段的向上(或向下)縮放乘法(或除法)不同。假設您的月利率爲每月 1%。如何將其轉換爲年利率?在這種情況下,時間倍數 = 12 個月/1 個月 = 12:
- 將月利率除以 100(得到 0.01)
- 加 1(得到 1.01)
- 將其計算爲時間倍數次方(即 1.01^12 = 1.1268)
- 從中減去 1(得到 0.1268)
- 乘以100,即爲年利率(12.68%)
這是任何涉及利率的估值模型中使用的年化利率。對於像布萊克-斯科爾斯這樣的標準期權定價模型,使用無風險的一年期國債利率。
值得注意的是,利率變動並不頻繁且幅度較小(通常增量爲 0.25%,或僅 25 個基點)。決定期權價格的其他因素(如標的資產價格、到期時間、波動性和股息收益率)變化更頻繁、幅度更大,與利率變化相比,這些因素對期權價格的影響相對更大。
要點
- 利率的變化直接影響期權定價,其計算由衆多複雜因素組成。
- 對於Black-Scholes等標準期權定價模型,使用無風險年化國債利率。
- 當利率上升時,看漲期權受益,而看跌期權價格受到負面影響。
利率如何影響看漲期權和看跌期權價格
爲了理解利率變化影響背後的理論,股票購買和同等期權購買之間的比較分析將是有用的。我們假設專業交易者用帶息借錢進行多頭頭寸交易,並通過空頭頭寸獲得生息資金。
看漲期權的利息優勢
以 100 美元的價格購買 100 股股票將需要 10,000 美元,假設交易者借錢進行交易,則需要支付這筆資金的利息。以 12 美元的價格購買 100 份合約的看漲期權僅需花費 1,200 美元。然而,利潤潛力將與多頭股票頭寸保持相同。
實際上,8,800 美元的差額將節省這筆貸款金額的支出利息。或者,節省下來的 8,800 美元資本可以保留在計息賬戶中,併產生利息收入——5% 的利息一年後將產生 440 美元。
因此,利率上升將導致貸款金額的支出利息節省或儲蓄賬戶利息收入的增加。兩者都對該看漲期權頭寸+儲蓄有利。實際上,看漲期權的價格上漲反映了利率上升帶來的好處。
看跌期權的利息劣勢
從理論上講,爲了從價格下跌中受益而做空股票將爲賣空者帶來現金。購買看跌期權也能從價格下跌中獲得類似的好處,但需要支付看跌期權溢價。這種情況有兩種不同的情況:通過做空股票收到的現金可以爲交易者賺取利息,而購買看跌期權所花費的現金則是應付利息(假設交易者借錢購買看跌期權)。
隨着利率上升,做空股票比買入看跌期權更有利可圖,因爲前者產生收入,而後者則相反。因此,看跌期權價格受到利率上升的負面影響。
羅希臘語
Rho是標準希臘語,用於衡量利率變化對期權價格的影響。它表示利率每變化 1%,期權價格將變化的量。假設看漲期權當前定價爲 5 美元,rho 值爲 0.25。如果利率增加 1%,則看漲期權價格將增加 0.25 美元(至 5.25 美元)或其 rho 值。同樣,看跌期權價格將減少其 rho 值。
由於利率變化不會頻繁發生,並且通常以 0.25% 爲增量,因此 rho 不被視爲主要希臘因子,因爲與其他因子(或希臘因子,如 delta、gamma)相比,它不會對期權價格產生重大影響。 、織女星或西塔)。
利率變化如何影響看漲期權和看跌期權價格?
以標的交易價格爲 100 美元的歐式價內(ITM)看漲期權爲例,行權價爲 100 美元,到期日爲一年,波動率爲 25%,利率爲 5%,使用 Black-Scholes 模型的看漲期權價格爲 12.3092 美元,看漲期權 rho 值爲 0.5035。具有類似參數的看跌期權價格爲 7.4828 美元,看跌期權 rho 值爲 -0.4482(情況 1)。
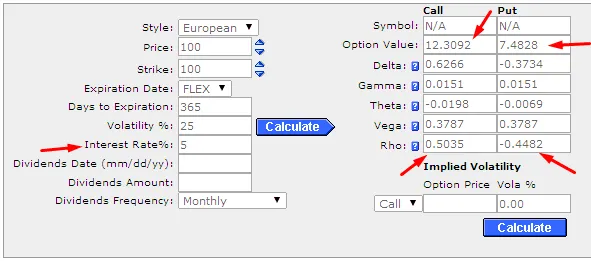
資料來源:芝加哥期權交易所(CBOE)
現在,我們將利率從 5% 提高到 6%,其他參數保持不變。
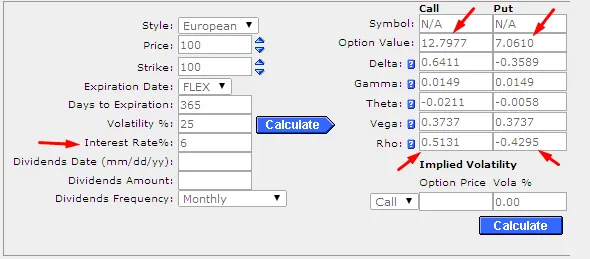
看漲期權價格已上漲至 12.7977 美元(變化爲 0.4885 美元),看跌期權價格已下跌至 7.0610 美元(變化爲 -0.4218 美元)。看漲期權價格和看跌期權價格的變化量與之前計算的看漲期權 rho (0.5035) 和看跌期權 rho (-0.4482) 值幾乎相同。 (分數差異是由於 BS 模型計算方法造成的,可以忽略不計。)
事實上,利率通常僅以 0.25% 的增量變化。舉一個現實的例子,我們將利率從 5% 改爲 5.25%。其他數字與情況1相同。
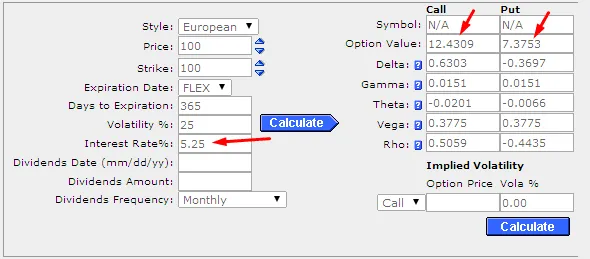
看漲期權價格增至 12.4309 美元,看跌期權價格降低至 7.3753 美元(看漲期權價格小幅變化 0.1217 美元,看跌期權價格小幅變化 - 0.1075 美元)。
可以看出,利率變化 0.25% 後,看漲期權和看跌期權價格的變化可以忽略不計。
利率可能會在一年內變化四次(4 * 0.25% = 1% 增加),即直到到期時間。儘管如此,此類利率變化的影響可能可以忽略不計(對於 12 美元的 ITM 看漲期權價格和 7 美元的 ITM 看跌期權價格,僅約 0.5 美元)。在一年中,其他因素的變化幅度可能要大得多,並且可能會對期權價格產生重大影響。
對虛值 (OTM) 和 ITM 期權進行類似的計算會產生類似的結果,但在利率變化後,期權價格僅觀察到微小的變化。
套利機會
是否有可能從預期利率變化的套利中受益?通常,市場被認爲是有效的,並且期權合約的價格已經被假定包含任何此類預期變化。
此外,利率的變化通常會對股票價格產生反向影響,這對期權價格的影響要大得多。總體而言,由於利率變化導致期權價格變化較小,套利收益難以利用。
綜述
期權定價是一個複雜的過程,並且不斷發展,儘管布萊克-斯科爾斯等流行模型已經使用了幾十年。影響期權估值的因素有多種,這可能導致期權價格在短期內出現很大的變化。看漲期權和看跌期權的溢價隨着利率的變化而受到相反的影響。然而,對期權價格的影響很小;期權定價對其他輸入參數的變化更加敏感,例如基礎價格、波動性、到期時間和股息收益率。