非線性SVM
上一節的算法針對的是輸入空間存在線性判別面的情況。對分類面是非線性函數的情況,理論上應將輸入空間通過某種非線性映射,映射到一個高維特徵空間,在這個空間中存在線性的分類規則,可以構造線性的最優分類超平面。但是這種方法帶來了兩個問題;一是概念上的問題,怎樣在如此高維的空間中找到一個推廣性好的分類超平面;二是技術上的問題,如何處理高維空間中的計算問題。
前面我們把尋找最優超平面最終歸結爲其Wolfe對偶問題,一個很重要的副產品就是找到了一個克服維數災難、解決技術上問題的絕好方法.如果數學上可以找到一個函數K : (Rn, Rn) -4 R,使得K(xi,xj)就等於xi,、xj在高維特徵空間中的映射的點積,那麼用K(xi,xj)代替Wolfe對偶問題中爲xi和xj的點積即可,計算量將會大大減少。事實上確實存在這樣的函數,Vapnik稱之爲卷積核函數,於是我們只需在輸入空間中計算卷積核函數,而不必知道非線性映射的形式,也不必在高維特徵空間中進行計算。
通過上一節已經看到,線性SVM是以樣本間的歐氏距離大小爲依據來決定劃分的結構的。非線性SVM中以卷積核函數代替內積後,相當於定義了一種廣義的距離,以這種廣義距離作爲劃分依據。也許並不一定所有的學習機器都要以樣本間距離作爲劃分依據,但是對於面臨的很多問題來說,把距離近的樣本劃分在一起確實是理所當然的。
我們自然會提出這樣的問題:怎樣選擇核函數?核函數的性質會對學習機器的推廣能力起決定作用嗎?幸運的是,實驗表明,採用不同種類核函數的學習機器表現出了大致相同的性能,它們找到的支持向量大致相同。多項式分類器、徑向基函數、兩層神經網絡等都是常用的SVM的核函數。
首先將輸入向量x通過映射Ψ:Rn→H映射到高維Hilbert空間H中。設核函數K滿足:K(xi,xj)=Ψ(xi)·Ψ(xj)
則二次規劃問題的目標函數變爲:
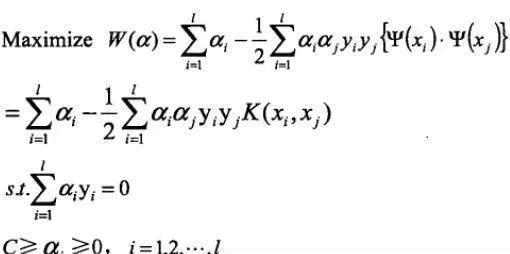
與線性情況有所不同的是:儘管在高維特徵空間中線性判別面的法向量w仍可表示成這個空間中支持向量的線性組合,但由於將輸入空間映射爲高維空間的是非線性映射,這種線性組合關係在輸入空間中不再表現爲線性組合,我們又不可能把工作樣本映射到高維空間再做判別,所以就需要重新考慮工作樣本的決策問題。在訓練完成之後,只需計算下列函數的符號即可:
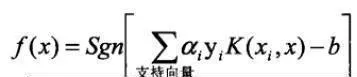
式中,b作爲偏移值,取值如下:
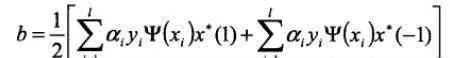
式中,x*(1)表示屬於第一類的某個(任一個)支持向量:x*(-1)表示屬於第二類的某個支持向量。
如果支持向量很多,則決策階段的計算量也會較大。所以在實際應用中,如果訓練集比較大而且得到的支持向量很多,在犧牲一點分類精度的情況下可以按一定規則捨棄一些支持向量來增加分類速度,這對時間有要求的實時系統是很有必要的。
通常,不需顯式地知道Ψ和H,只需選擇合適的核函數K就可以確定支持向量機。Mercer定理給出了核的數K滿足上式的充要條件:
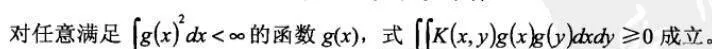
選擇不同形式的核函數K就可以生成不同的支持向量機,常用的有以下幾種:
(1)多項式SVM(d=1時候爲線性核):K(x,y=[(x·Y)+1]d。
(2)徑向基函數SVM: K(x,y)=e-‖x-y‖²/2σ²。
(3)Sigmoid函數SVM: K(x,y)=tanh(k(x·y)+δ)。
概括地說,支持向量機就是首先通過用內積函數定義的非線性變換將輸入空間變換到一個高維空間,然後求(廣義)最優分類面。SVM分類函數形式上類似於一個神經網絡,輸出的是若干中間層節點的線性組合,而每個中間層節點對應於輸入樣本與一個支持向量的內積,如圖13-1所示。
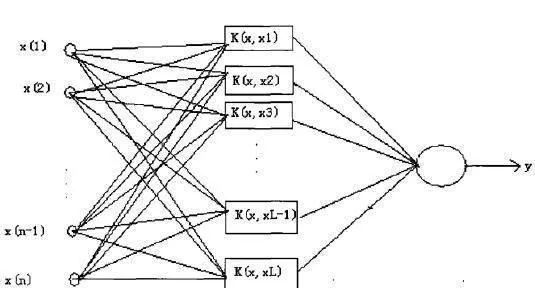
圖13-1 支持向最機結構
其中輸入層用於存儲輸入數據,並不做任何加工運算:中間層是通過對樣本集的學習,選擇K(X, Xi,),i=1,2,3,…,L;最後一層就是構造分類函數:
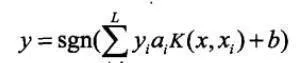
整個過程等價於在特徵空間中構造一個最優超平面。
支持向量機的作用之一就是分類,根據分類的任務,可以劃分爲一分類、二分類及多分類。對於多類分類問題,可以用若干種手法將其分解爲若干個二分類問題疊加。