1、三分康託集
1883年,德國數學家康託(GCantor )提出瞭如今廣爲人知的三分康託集。三分康託集是很容易構造的,然而它卻顯示出許多最典型的分形特徵。它是從單位區間出發,再由這個區間不斷地去掉部分子區間的過程構造出來的,如圖14-1所示。

圖14-1 三分康託集
其詳細構造過程如下:
(1)把閉區間[0,1]平均分爲3段,去掉中間的1/3部分段,則只剩下兩個閉區間[0,1/3]和[2/3,1]。
(2)再將剩下的兩個閉區間各自平均分爲3段,同樣去掉中間的區間段,這時剩下4段閉區間:[0,1/9], [2/9,1/3], [2/3,7/9]和[8/9,1]。
(3)重複刪除每個小區間中間的1/3段。如此不斷地分割下去,最後剩下的各個小區間段就構成了三分康託集。三分康託集的Hausdorff維數是0.6309。
Koch曲線
1904年,瑞典數學家柯赫構造了Koch曲線幾何圖形。Koch曲線大於一維,具有無限的長度,但是又小於二維,並且生成的圖形的面積爲零。它和三分康託集一樣,是一個典型的分形。根據分形的次數不同,生成的Koch曲線也有很多種,如三次Koch曲線、四次Koch曲線等。
次Koch曲線的構造過程主要分爲三大步驟:
(1)給定一個初始圖形—一條線段。
(2)將這條線段中間的1/3處向外折起。
(3)按照第(2)步的方法不斷地把各段線段中間的1/3處向外折起。這樣無限地進行下去,最終即可構造出Koch曲線。其圖例構造過程如圖14-2所示。
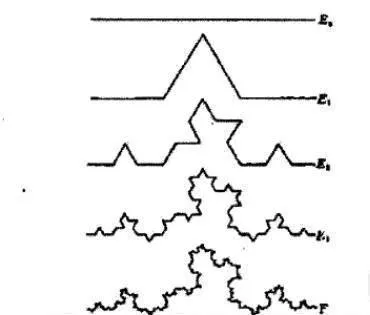
圖14-2 Koch曲線
Julia集
Julia集是由法國數學家Gaston Julia和Pierre Faton在發展了複變函數迭代的基礎理論後獲得的。Julia集也是一個典型的分形,只是在表達上相當複雜,難以用古典的數學方法描述。
Julia集由一個複變函數:ƒ(z)z²+c(c爲常數)生成,儘管這個複變函數看起來很簡單,然而它卻能夠生成很複雜的分形圖形。如圖14-3所示爲Julia集生成的圖形,由於c可以是任意值,所以當c取不同的值時,生成的Julia集的圖形也不相同。

圖14-3 Julia集生成的圖形