期權的剖析

期權交易者必須瞭解期權的複雜性。瞭解期權的構成結構可讓交易者做出合理判斷，併爲他們提供更多執行交易的選擇。

希臘人

“希臘值”提供了有關風險管理的重要信息，有助於重新平衡投資組合以實現所需的風險敞口（例如Delta對沖）。每個希臘值衡量投資組合對特定基礎因素的微小變化的反應，從而可以檢查單個風險。

Delta 衡量的是期權價值相對於標的資產價格變化的變化率。

Gamma衡量的是相對於標的資產價格變化的 delta 的變化率。

Lambda或彈性與期權價值相對於標的資產價格百分位變化的百分位變化有關。這提供了一種計算槓桿的方法，槓桿也可以稱爲槓桿率。

Theta計算期權價值對時間流逝的敏感度，這一因素稱爲“時間衰減”。

Vega衡量波動性敏感性。Vega 衡量期權相對於標的資產波動性的價值。

Rho評估期權價值對利率的反應性：它是期權價值相對於無風險利率的度量。

因此，使用Black Scholes 模型（被認爲是評估期權的標準模型），希臘值相當容易確定，並且對於日內交易者和衍生品交易者非常有用。對於測量時間、價格和波動性，delta、theta 和 vega 是有效的工具。

期權的價值直接受“到期時間”和“波動性”的影響，其中：

與看跌期權相比，標的證券的價格對看漲期權的價值有不同的影響。

交易者購買期權合約並向期權合約賣方支付預付款時，就會發生這種情況。期權溢價會有所不同，具體取決於計算時間和購買的期權市場。根據以下標準，溢價甚至可能在同一市場內有所不同：

期權是價內、平價還是價外期權？價內期權的賣出溢價更高，因爲合約已經盈利，合約買方可以立即獲得這筆利潤。相反，平價或價外期權的買入溢價更低。
合約的時間價值是多少？期權合約一旦到期，就變得毫無價值，因此理所當然的是，距離到期日的時間越長，溢價就越高。這是因爲合約包含額外的時間價值，因爲期權有更多時間可以獲利。
市場波動水平如何？如果期權市場波動性更大，溢價就會更高，因爲從期權中獲利的可能性更大。反之亦然——波動性越低，溢價就越低。期權市場的波動性是通過將各種價格範圍（長期、近期和預期價格範圍是必需的數據）應用於一系列波動性定價模型來確定的。

看漲期權和看跌期權在達到其共同的 ITM、ATM 和 OTM 執行價格時，並不具有匹配的價值，這是由於直接和相反的影響，它們在不規則的分佈曲線之間擺動（見下面的例子），從而變得不均勻。

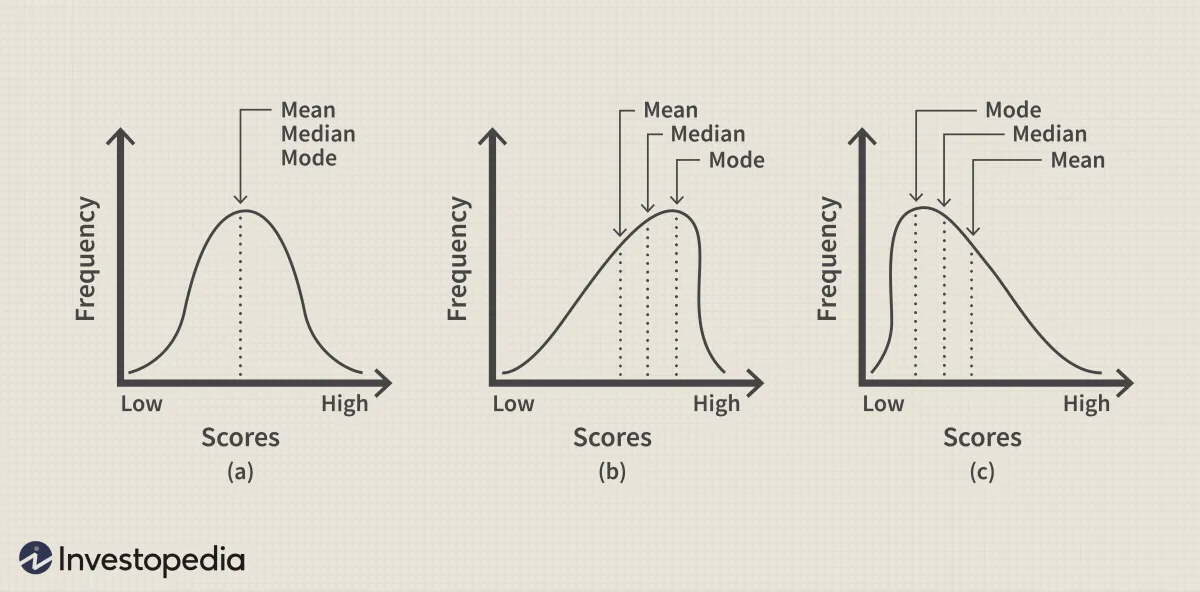
執行價格是執行價格的數目，執行價格之間的增量由產品交易的交易所決定。

在使用歷史波動率和隱含波動率進行交易時，需要注意它們所隱含的差異：

歷史波動率計算標的資產在特定時間段內的波動率，其中價格變化的年度標準差以百分比表示。它衡量所選時間範圍內，在信息系列中每個計算日期之前，標的資產在指定數量的前交易日（可修改期間）的波動程度。

隱含波動率是對標的資產交易量的未來綜合估計，用於衡量資產的每日標準差在計算時間和期權到期日之間預計會如何變化。在分析期權價值時，隱含波動率是日內交易者要考慮的關鍵因素之一。在計算隱含波動率時，會使用期權定價模型，其中會考慮期權溢價的成本。

日內交易者可以利用三種常用的理論定價模型來計算隱含波動率。這些模型是 Black-Scholes、Bjerksund-Stensland 和二項式模型。計算是使用算法完成的——通常使用平價或最近平價看漲期權和看跌期權。