量化投資 | 2022年8月15日
分形理論的誕生接近30年，它對多種學科的影響是極其巨大的.分形理論在生物學、地球物理學、物理學和化學、天文學、材料科學、計算機圖形學、語言學與情報學、信息科學、經濟學等領域都有廣泛的應用。
在量化投資中，分形也具有重要的價值，例如，一般來說，股票價格變動圖完全是隨機的，因此使人感到幾乎無規律可循。但若從統計學觀點解析這一變動，就會發現有很好的規律。
(1)每個單位時間內的股票價格變動分佈，服從特性指數D≈1.7的對稱穩定分佈。
(2)單位時間不論取多大或多小，其分佈也是相似的，也就是說，適當地改變尺度，就可成爲同樣的分佈。
關於穩態分佈，只討論與分形有關的一些性質。若把單位時間T之間的股票價格變動x的分佈密度記爲P(x)，則下述關係成立：
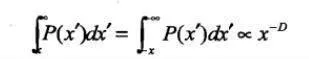
此關係式表示股票價格變動的大小分佈爲分形。例如，一天的股票價格變動在x元以上，比2x元以上的變動次數多2的1.7倍≈3.2倍。
法則(2)表示股票價格變動在時間上也是分形的。一天的股票價格變動圖形與一年的股票價格變動圖形相比，不同的只是股票價格的尺度，而對變動情況則很難加以區別。
如圖4-16所示。 圖4-16 金瑞科技走勢圖圖4-16是金瑞科技(600390）的一段走勢圖，圖中有標記的地方是一個前高後低的紅柱組閤形態。前麵我們講瞭太多的綠柱組閤形態。下麵我們看一下前高後低的紅柱形態。從實際應用上來說，它們之間的原理是一樣的，隻是和綠柱的正好相反。紅柱的高柱峰代錶的是股價上漲幅度大。
在很多時候，下跌趨勢持續的時間、纍計下跌的幅度是遠遠超齣我們想象的，如果不藉助於可靠的指標形態，我們往往在其下跌途中有“抄底”入場的衝動，而這種不明智的決定將使得我們隨後的操作十分被動，要麼是割肉離場，這將是一筆失敗的交易，將嚴重打擊我們的操作信心;要麼是無奈地等待，這將錯過很多中短綫買股時機，
分形維數歐氏幾何學有着幾千年的歷史，它研究的是一些規整的圖形，如直線、圓、橢圓、菱形、正方形、立方體、長方體、球體等。這些不同類型的曲線和形狀都有一個共同的基礎—歐氏幾何，即它們可以被定義爲代數方程(例如，Ax+By+Cz=D)或微分方程的解集。
新股民在選股時有時易犯教條主義錯誤。有些理論指導投資者只買下跌的股票而不是賣上漲的股票，問題是這樣就能迴避風險嗎?要知道股票是可以一跌再跌的。另一方面，在某些股票一漲再漲之時眼看着可以獲得的利潤而不採取行動也是痛心的錯誤。
在現實交易當中，我們會發現短線交易是一種成本非常高的交易方法，除了技術指標本身的一些天然缺陷所導致的必然錯誤之外，損失的還有證券交易所扣除的大量手續費用及政府徵收的印花稅。有位朋友在年頭好的時候，短線底利曾達到12萬元，但是付出的各種費用就有7萬元多。
KDJ指標的金叉形態當股價經過一段很長時間的低位盤整行情，並且K、D、J三線都處於50線以下時，一旦J線和K線幾乎同時向上突破D線時，表明股市即將轉強，股價跌勢已經結束，將止跌朝上，可以開始買進股票，進行中長線建倉。這是KDJ指標“黃金交叉”的一種形式。
均綫係統空頭排列止贏法則技術特徵第一、在1分鍾的分析周期上，股價反彈失敗後，拉齣一根大陰綫，如下圖所示。第二、隨後股價直接擊穿均綫係統所有均綫，均綫係統呈現為空頭排列。第三、此時，1分鍾的中長期的均綫組閤對股價的上行構成瞭反壓，製約著股價上行。
我們繼續深入關於冠軍魔咒的研究，進入一個更加重要但是更少有人研究的領域——失敗之後怎麼辦？儘管冠軍容易跌倒，但我們也有理由相信冠軍還有可能再爬起來。事實上，2009年的冠軍L先生、2010年的冠軍C先生等，都有過產品淨值被腰斬之後，再度騰飛的事例。
死亡榖是指股價或指數見頂迴落時，帶動5日均綫下穿10日均綫和20日均綫，10日均綫下穿20日均綫，三條均綫交叉形成的尖頭嚮下的不規則三角形。其中三個交叉中，至少有兩個是死亡交叉。因其外形像山榖，後市看跌，所以稱為死亡榖。死亡榖是與銀山榖、金山榖相對的一種技術形態，技術形態的構成和特徵相同，隻是方嚮和技術含義相反。
下麵是筆者的一個實戰案例:2009年6月湖北金環以漲停開盤，雖然接近11點時漲停闆被打開，但是15分鍾後再次封死漲停，再也沒被打開。這引起筆者的注意，經過分析，它符閤箱體形態，並以漲停形式突破，突破時大幅度放從，且均綫還符閤粘閤共振嚮上形態，所以筆者認定該股後期會有很好的錶現。
什麼是錯誤交易？錯誤交易是指股票交易與當前市場價格的偏差如此之大，以至於被認為是錯誤的。錯誤交易是由多種因素引起的，包括計算機故障或人為錯誤。這些交易經常被逆轉或中斷，因為它們不能反映證券的真實價格，並且它們會影響或導致其他股票或交易所的錯誤交易。關鍵點錯誤交易是指與當前市場價格相差很大以至於被視為錯誤的交易。
什麼是零加刻度？零加價或零上漲是一種證券交易，以與前一交易相同的價格執行，但價格高於不同價格的最後一筆交易。例如，如果連續的交易發生在 10 美元、10.01 美元和 10.01 美元，則後面的交易將被視為零加價或零上漲交易，因為它與前一交易的價格相同，但價格高於以不同價格進行的最後一筆交易。
什麼是成長股？成長股是指公司的任何股票，預計其增長率將大大高於市場平均增長率。這些股票一般不派息。這是因為成長型股票的發行人通常是希望將其積累的任何收益再投資以在短期內加速增長的公司。當投資者投資於成長型股票時，他們預計他們將在未來最終出售股票時通過資本收益來賺錢。
什麼是優先股？優先股，通常稱為優先股，是公司股票的股份，在普通股股利發放之前已向股東支付股利。如果公司破產，優先股股東有權在普通股股東之前從公司資產中獲得報酬。大多數優先股都有固定的股息，而普通股一般沒有。優先股股東通常也不擁有任何投票權，但普通股股東通常擁有。
什麼是反稀釋條款？反稀釋條款是可轉換優先股和一些期權中的條款，以幫助保護投資者免受可能損失價值的投資。當新發行的股票以低於早期投資者購買同一股票的價格進入市場時，就會發生股權稀釋。反稀釋條款也稱為反稀釋條款、認購權、認購特權或優先購買權。了解反稀釋條款反稀釋條款起到緩衝作用，以保護投資者免受其股權頭寸被稀釋或價值降低。
什麼是流通股？流通股是可用於交易特定股票的股票數量。低流通股是指股票數量較少的股票。流通股的計算方法是從公司的總流通股中減去密切持有的股票和限制性股票。封閉持有的股票是由內部人士、大股東和員工持有的股票。限制性股票是指由於臨時限制（例如首次公開募股（IPO）後的鎖定期）而無法交易的內幕股票。